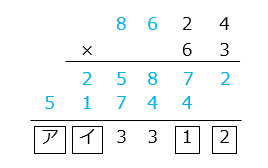算数【基本】四則計算（文章題）

問１

（１）ある数に2.5を足した数を3倍して、そこから27を引くと21になりました。ある数を求めなさい。

答え（１）

13.5

解き方（１）

ある数を□として、問題文を式にすると、
( □ + 2.5 ) × 3 – 27 = 21
( □ + 2.5 ) × 3 = 21 + 27 = 48
□ + 2.5 = 48 ÷ 3 = 16
□ = 16 – 2.5 = 13.5

（２）\(\dfrac{25}{36}\) にある数を足してから \(1\dfrac{13}{36}\) で割ると1になります。ある数を求めなさい。

答え（２）

\(\dfrac{2}{3}\)

解き方（２）

ある数を□として、問題文を式にすると、
( \(\dfrac{25}{36}\) + □ ) ÷ \(\dfrac{49}{36}\) = 1

( \(\dfrac{25}{36}\) + □ ) × \(\dfrac{36}{49}\) = 1　※分数のわり算はかけ算に直してから次に進む

\(\dfrac{25}{36}\) + □ = 1 ÷ \(\dfrac{36}{49}\)

\(\dfrac{25}{36}\) + □ = \(\dfrac{49}{36}\)

□ = \(\dfrac{49}{36}\) – \(\dfrac{25}{36}\) = \(\dfrac{24}{36}\) = \(\dfrac{2}{3}\)

（３）ある数に6をかけるところを間違えて6を足したところ、正しい答えと同じになりました。ある数を求めなさい。

答え（３）

1.2（または \(1\dfrac{1}{5}\) ）

解き方（３）

ある数を□として、問題文を式にすると、
□ × 6 = □ + 6
□ × 6 – □ = 6
□ × ( 6 – 1 ) = 6
□ × 5 = 6
□ = 6 ÷ 5 = 1.2

（４）\(\dfrac{17}{32}\) の分母と分子のどちらにもある数を足すと、\(\dfrac{8}{13}\) になります。ある数を求めなさい。

答え（４）

7

解き方（４）

ある数を□として、問題文を式にすると、
\(\dfrac{17\ +\ □}{32\ +\ □}\) = \(\dfrac{8}{13}\)
13 × ( 17 + □ ) = 8 × ( 32 + □ )
221 + 13 × □ = 256 + 8 × □
13 × □ – 8 × □ = 256 – 221
( 13 – 8 ) × □ = 35
5 × □ = 35
□ = 7

（５）次の式の□に当てはまる数を答えなさい。

①

答え（５）- ①

ア：8　イ：7　ウ：1

解き方（５）- ①

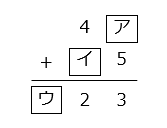
\(\boxed{ア}\) + 5 の一の位が 3 になるのは、\(\boxed{ア}\) = 8
\(\boxed{ア}\) + 5 = 8 + 5 = 13
よって、1 + 4 + \(\boxed{イ}\) = 5 + \(\boxed{イ}\) の一の位が 2 になるのは、\(\boxed{イ}\) = 7
5 + \(\boxed{イ}\) = 5 + 7 = 12 より、\(\boxed{ウ}\) = 1

②

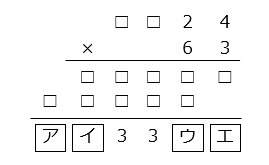
答え（５）- ②

ア：5　イ：4　ウ：1　エ：2

解き方（５）- ②

確定できる値を入力する。

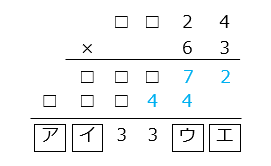
よって、\(\boxed{エ}\) = 2、\(\boxed{ウ}\) = 1

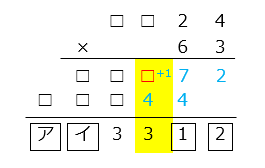
1 + □ + 4 の一の位が 3 のとき、□ = 8 (1 + 8 + 4 = 13)

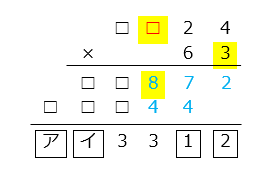
3 × □ の一の位が 8 のとき、□ = 6 (3 × 6 = 18)

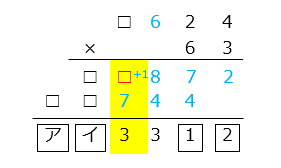
1 + □ + 7 の一の位が 3 のとき、□ = 5 (1 + 5 + 7 = 13)

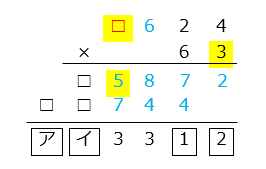
5は、前の 3 × 6 = 18 の十の位の1が繰り上がっているので、3 × □ の一の位は 4
このとき、□ = 8 (3 × 8 = 24)

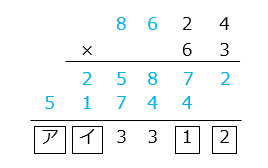
よって、\(\boxed{イ}\) = 4、\(\boxed{ア}\) = 5

③ すべての□に値を入れなさい。

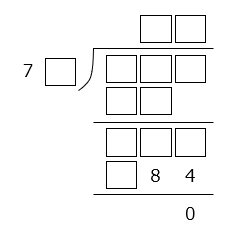
答え（５）- ③

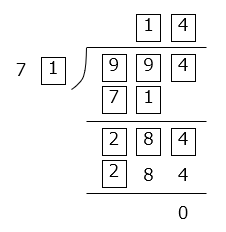
解き方（５）- ③

確定できる値を入力する。

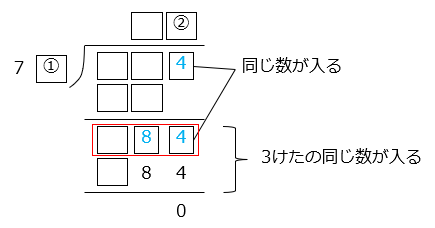
7 \(\boxed{①}\) × \(\boxed{②}\) = \(\boxed{　　}\) となる。
かけ算をして一の位が4になるのは、1 × 4 または 2 × 2
71 × 4 = 284
72 × 2 = 144 ⇒ 下2けたが異なる
74 × 1 = 74 ⇒ 3けたでない
よって、\(\boxed{①}\) = 1、\(\boxed{②}\) = 4

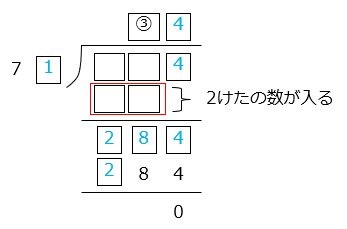
71 × \(\boxed{③}\) = \(\boxed{　　}\) となる。
よって、\(\boxed{③}\) = 1

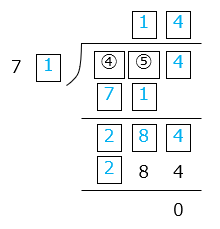
\(\boxed{④}\) \(\boxed{⑤}\) – 71 = 28
よって、\(\boxed{④}\) = 9、\(\boxed{⑤}\) = 9

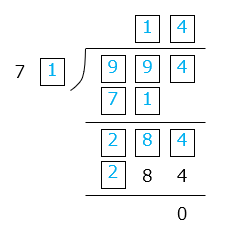
（６）□に +、-、×、÷ のいずれかを入れて、式を完成させなさい。

8 □ 6 □ 4 □ 2 = 10

答え（６）

8 × 6 ÷ 4 – 2 = 10　または、8 – 6 + 4 × 2 = 10

問２

（１）\(\dfrac{4}{5}\)、0.7、\(\dfrac{13}{18}\) を大きい方から順に並べなさい。

答え（１）

\(\dfrac{4}{5}\)、\(\dfrac{13}{18}\)、0.7

解き方（１）

\(\dfrac{4}{5}\)、0.7、\(\dfrac{13}{18}\)

すべて分数に直す ⇒ \(\dfrac{4}{5}\)、\(\dfrac{7}{10}\)、\(\dfrac{13}{18}\)

分母を最小公倍数でそろえる ⇒ \(\dfrac{72}{90}\)、\(\dfrac{63}{90}\)、\(\dfrac{65}{90}\)

\(\dfrac{72}{90}\) ＞ \(\dfrac{65}{90}\) ＞ \(\dfrac{63}{90}\)

\(\dfrac{4}{5}\) ＞ \(\dfrac{13}{18}\) ＞ 0.7

（２）分母が30で、\(\dfrac{7}{18}\) より大きく、\(\dfrac{23}{45}\) より小さい分数は何個ありますか。ただし、約分できるものは除きます。

答え（２）

1個

解き方（２）

\(\dfrac{7}{18}\)、\(\dfrac{23}{45}\)

分母を18と30と45最小公倍数90でそろえる ⇒ \(\dfrac{35}{90}\)、\(\dfrac{46}{90}\)

\(\dfrac{35}{90}\) より大きく、\(\dfrac{46}{90}\) より小さい分母が30の分数の分子の値は、分母を90とすると、分子は35より大きく、46より小さい3の倍数となる

\(\dfrac{36}{90}\)、\(\dfrac{39}{90}\)、\(\dfrac{42}{90}\)、\(\dfrac{45}{90}\)

⇒ \(\dfrac{2}{5}\)、\(\dfrac{13}{30}\)、\(\dfrac{7}{15}\)、\(\dfrac{1}{2}\)

よって、1個

問３

（１）岡山県産の桃が2個で640円、和歌山県産の桃が3個で950円で売られているとき、1個当たりの値段が安いのはどちらですか。

答え（１）

和歌山県産

解き方（１）

1個当たりの値段は、
岡山県産　640 ÷ 2 = 320(円)
和歌山県産　950 ÷ 3 = 316.6…(円)
和歌山県産の方が安い

（２）コインを投げて、表が出ると8点、裏が出ると2点もらえます。コインを15回投げたところ、表が9回でました。このとき、得点は何点になりますか。

答え（２）

84点

解き方（２）

表が9回、裏が 15- 9 = 6(回)出たので、得点は、
9 × 8 + 6 × 2 = 72 + 12 = 84(点)

（３）えんぴつ1本が72円、ボールペン1本が150円です。100本のえんぴつの値段と等しくなる、ボールペンの本数を答えなさい。

答え（３）

48本

解き方（３）

えんぴつ100本の値段は、72 × 100 = 7200(円)
同じ値段になるときのボールペンの本数は、
7200 ÷ 150 = 48(本)

（４）図のように、たて・横5列ずつの表があります。この表に1から25までの整数を1つずつあてはめ、たて・横・ななめのどの5つの整数を合計しても和が等しくなるようにします。

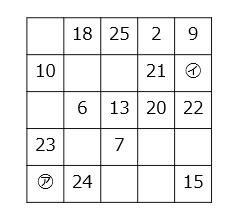
① 1列の5つの整数の合計はいくらになりますか。

答え（４）- ①

65

解き方（４）- ①

1列の合計を□とすると、次の式が成り立つ。
5 × □ = 1 + 2 + ・・・ + 25
1 + 2 + ・・・ + 25
= ( 1 + 2 + ・・・ + 10 ) + { 10 × 10 + ( 1 + 2 + ・・・ + 10 )} + { 20 × 5 + ( 1 + 2 + 3 + 4 + 5 )}
= 55 + ( 100 + 55 ) + ( 100 + 15 ) = 325
5 × □ = 325
□ = 65
※「1 + 2 + ・・・ + 9 = 45」、「1 + 2 + ・・・ + 10 = 55」は覚えておくと便利です！

【別解１】等差数列の和を求める式を利用する
「1 + 2 + ・・・ + 25」を等差数列の和と考えると、
1 + 2 + ・・・ + 25
= 25 × ( 1 + 25 ) ÷ 2 = 325

【別解２】たて・横が奇数の表の場合
表の中心の数字は必ず整数の真ん中の数になります。今回は1～25の真ん中の13です。
たて・横5なので、13 × 5で求めることができます。

② ㋐、㋑にあてはまる整数を求めなさい。

答え（４）- ②

㋐：17　㋑：3

解き方（４）- ②

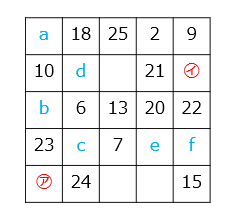
a = 65 – ( 18 + 25 + 2 + 9 ) = 65 – 54 = 11
b = 65 – ( 6 + 13 + 20 + 22 ) = 65 – 61 = 4
㋐ = 65 – ( 11 + 10 + 4 + 23 ) = 65 – 48 = 17
c = 65 – ( 9 + 21 + 13 + 17 ) = 65 – 60 = 5
d = 65 – ( 18 + 6 + 5 + 24 ) = 65 – 53 = 12
e = 65 – ( 11 + 12 + 13 + 15 ) = 65 – 51 = 14
f = 65 – ( 23 + 5 + 7 + 14 ) = 65 – 49 = 16
㋑ = 65 – ( 9 + 22 + 16 + 15 ) = 65 – 62 = 3

（５）図のように、幅3mの掲示板に幅22cmのプリントを1列にはっていきます。掲示板のはしとプリントの間かく、プリントとプリントの間かくは10cm以上開ける必要があります。このとき、最大何枚のプリントをはることができますか。

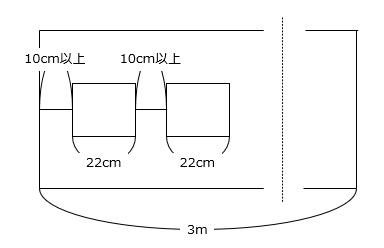
答え（５）

9枚

解き方（５）

間かくが10cmのとき、枚数は最大になる。

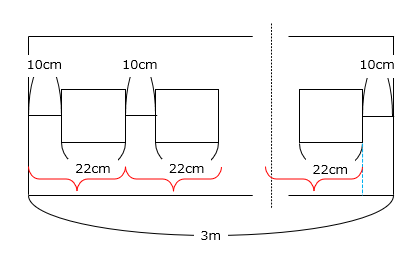
( 300 – 10 ) ÷ ( 10 + 22 )
= 290 ÷ 32 = 9あまり2
よって、9枚

問４

（１）( a, b ) はaの3倍とbの2倍の和、＜ a, b ＞はaの3倍とbの2倍の差、【 a, b 】はaとbの積を表します。

このとき、【 ( \(\dfrac{1}{5}\), \(\dfrac{3}{4}\) ), ＜ \(\dfrac{1}{2}\), \(\dfrac{1}{18}\) ＞】を求めなさい。

答え（１）

\(2\dfrac{11}{12}\)

解き方（１）

( \(\dfrac{1}{5}\), \(\dfrac{3}{4}\) )

= \(\dfrac{1}{5}\) × 3 + \(\dfrac{3}{4}\) × 2

= \(\dfrac{3}{5}\) + \(\dfrac{3}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{15}{10}\) = \(\dfrac{21}{10}\)

＜ \(\dfrac{1}{2}\), \(\dfrac{1}{18}\) ＞

= \(\dfrac{1}{2}\) × 3 – \(\dfrac{1}{18}\) × 2

= \(\dfrac{3}{2}\) – \(\dfrac{1}{9}\) = \(\dfrac{27}{18}\) – \(\dfrac{2}{18}\) = \(\dfrac{25}{18}\)

【 ( \(\dfrac{1}{5}\), \(\dfrac{3}{4}\) ), ＜ \(\dfrac{1}{2}\), \(\dfrac{1}{18}\) ＞】=【 \(\dfrac{21}{10}\), \(\dfrac{25}{18}\) 】

= \(\dfrac{\cancelto{7}{21}}{\cancelto{2}{10}}\) × \(\dfrac{\cancelto{5}{25}}{\cancelto{6}{18}}\) = \(\dfrac{35}{12}\) = \(2\dfrac{11}{12}\)

（２）A○BはAをB回かけることを表し、A△BはAをBで割ったときの余りを表します。また、A□BはAとBの最大公約数を表します。

このとき、｛( 36□54 ) △4 ｝○4を求めなさい。

答え（２）

16

解き方（２）

36□54 → 36と54の最大公約数は18
( 36□54 ) △4 = 18△4 → 18 ÷ 4 = 4 あまり 2 より2
｛( 36□54 ) △4 ｝○4 = 2 ○ 4 = 2 × 2 × 2 × 2 = 16

（３）A◎B = A × B + A + B + 1 と計算することにします。

① ( 12◎5 )◎3 を計算しなさい。

答え（３）- ①

316

解き方（３）- ①

12◎5 = 12 × 5 + 12 + 5 + 1 = 78
( 12◎5 ) ◎3 = 78◎3 = 78 × 3 + 78 + 3 + 1 = 316

② ( 3◎□ )◎6 = 287となるとき、□に当てはまる数を求めなさい。

答え（３）- ②

9

解き方（３）- ②

( 3◎□ ) ◎ 6 = 287
( 3◎□ ) × 6 + ( 3◎□ ) + 6 + 1 = 287
( 3◎□ ) × 7 + 7 = 287
( 3◎□ ) × 7 = 280
3◎□ = 40
3 × □ + 3 + □ + 1 = 40
4 × □ + 4 = 40
4 × □ = 36
□ = 9

（４）A△BはAをBで割ったときの余りを表します。

( 52△7 ) × ( 52△9 ) × ( 52△11 ) × ( 52△13 ) を計算しなさい。

答え（４）

0

解き方（４）

52△13 → 52 ÷ 13 = 4 あまり 0 より0
( 52△7 ) × ( 52△9 ) × ( 52△11 ) × ( 52△13 )
= 3 × 7 × 8 × 0 = 0

📢( 52△13 )が0とわかれば他は計算しなくてもよい。