- ポイント
- 【食塩水濃度計算まとめ表】(気に入ったら使ってください)
この表は本サイトが推奨する方法です。
表には次のように値を入れます。食塩 水 濃度(%) 食塩の割合 水の割合 量(g) 食塩の量 水の量 食塩水の量(g) 食塩水
この表は5個のわくがありますが、少なくとも1つ量(g)の数値がわかっていて、5個のわくのうち2個数値があればすべて計算で求めることができます。
詳細は【基本】ページを参照してください!
5個のわくのうち2個数値がない場合は、面積図を利用しましょう!!
【食塩の面積図】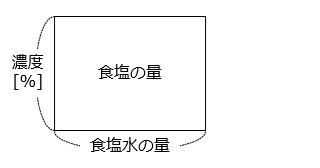
問1
ある容器には 20 % の食塩水が 300 g 入っています。この容器に 10 % の食塩水を \(\boxed{ア}\) g 入れると \(\boxed{イ}\) % の食塩水ができます。しかし、まちがえて \(\boxed{ア}\) g の水を入れてしまったので、 6 % の食塩水ができました。
□に当てはまる数を求めなさい。
- 答え
- ア:700 イ:13
- 解き方
- 20 % の食塩水 300 g に入っている食塩の量は、
20 % 80 % ? g 300 g
300 × 0.2 = 60 [g]
水を入れて 6 % の食塩水になったので、6 % 94 % 60 g \(\boxed{ア}\) g ( 300 + \(\boxed{ア}\) ) g
したがって、300 + \(\boxed{ア}\) = 1000
\(\boxed{ア}\) = 700 [g]
10 % の食塩水 700 g に入っている食塩の量は 0.1 × 700 = 70 [g] より、\(\boxed{イ}\) % % ( 60 + 70 ) g g ( 300 + 700 ) g
\(\boxed{イ}\) = 130 ÷ 1000 × 100 = 13 [%]
問2
15 % の食塩水 300 g のうち、何 g かを取り出した後に、同じ重さの水をもどすと、濃度が 6 % になりました。取り出した食塩水は何 g ですか。
- 答え
- 180 g
- 解き方
- 15 % の食塩水 300 g に入っている食塩の量は 300 × 0.15 = 45 [g] 、6 % の食塩水 300 g に入っている食塩の量は 300 × 0.06 = 18 [g] より、取り出した 15 % の食塩水には 45 – 18 = 27 [g] の食塩が入っていたと考えられる。
15 % % 27 g g □ g
□ = 27 ÷ 0.15 = 180 [g]
問3
濃度が 10 %、6 %、□ % の 3 種類の食塩水を 1:1:3 の割合で混ぜると 5 % の食塩水ができます。
□に当てはまる数を求めなさい。
- 答え
- 3
- 解き方
- 10 % と 6 % の食塩水を 1:1 で混ぜたとき、△ % の食塩水ができるとすると、
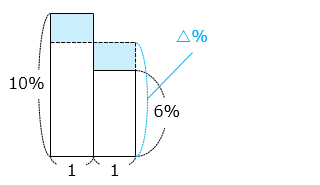
( 10 – △ ) × 1 = ( △ – 6 ) × 1
2 × △ = 16
△ = 8 [%]
よって、10 %、6 %、□ % の 3 種類の食塩水を 1:1:3 の割合で混ぜることは、8 % と □ % の 2 種類の食塩水を 2:3 の割合で混ぜることと同じなので、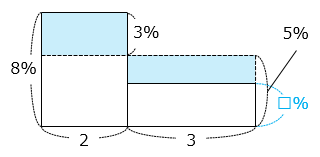
3 × 2 = ( 5 – □ ) × 3
3 × □ = 9
□ = 3 [%]
【別解】比の問題として考える
10 % の食塩水を① g 混ぜるとすると、6 % の食塩水は ① g、□ % の食塩水は③ g、できた 5 % の食塩水は ① + ① + ③ = ⑤ [g] と表すことができる。
よって、食塩の量に注目すると、次の式が成り立つ。
0.1 × ① + 0.06 × ① + \(\dfrac{□}{100}\) × ③ = 0.05 × ⑤
10 × ① + 6 × ① + □ × ③ = 5 × ⑤
⑩ + ⑥ + □ × ③ = ㉕
③ × □ = ⑨
□ = 3 [%]
問4
12 % の食塩水 200 g に水を入れて、8 % の食塩水を作るつもりでしたが、まちがえて水のかわりに 3 % の食塩水を入れてしまいました。何 % の食塩水になりましたか。
- 答え
- 9 %
- 解き方
- 12 % の食塩水 200 g に入っている食塩の量は 200 × 0.12 = 24 [g] より、8 % の食塩水を作るために必要な水の量を □ g とすると、
8 % % 24 g g ( 200 + □ ) g
200 + □ = 24 ÷ 0.08 = 300
□ = 100 [g]
3 % の食塩水 100 g に入っている食塩の量は 100 × 0.03 = 3 [g] より、できた食塩水 300 g に入っている食塩の量は 24 + 3 = 27 [g] なので、□ % 27 g 300 g
27 ÷ 300 × 100 = 9 [%]
問5
食塩水 A の濃度は、食塩水 B の濃度の 4 倍です。食塩水 A と食塩水 B を 4:1 の割合で混ぜると 10.2 % の食塩水ができました。食塩水 B の濃度は何 % ですか。
- 答え
- 3 %
- 解き方
- 食塩水 B の濃度を□ % とすると、A の濃度は 4 × □ [%] と表すことができる。
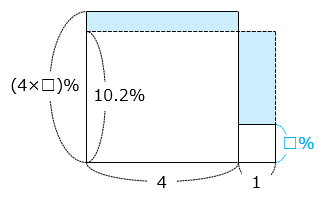
( 4 × □ – 10.2 ) × 4 = ( 10.2 – □ ) × 1
17 × □ = 10.2 + 4 × 10.2 = 5 × 10.2 = 51
□ = 3 [%]
問6
3 つのビーカー A、B、C があります。A には 4 % の食塩水が 250 g、B には濃度が分からない食塩水が 200 g、C には水が 150 g 入っています。
(1)A、B、C の 3 つをすべて混ぜ合わせたところ、6 % の食塩水になりました。B の濃度は何 % でしたか。
- 答え(1)
- 13 %
- 解き方(1)
- A、B、C をすべて混ぜ合わせてできた食塩水に入っている食塩の量は、
( 250 + 200 + 150 ) × 0.06 = 36 [g]
A の食塩水に入っている食塩の量は 250 × 0.04 = 10 [g]
よって、B の食塩水に入っている食塩の量は、
36 – 10 = 26 [g]
B の濃度は、
26 ÷ 200 × 100 = 13 [%]
(2)(1)のあと、水を蒸発させて 10 % の食塩水を作りました。蒸発させた水の量は何 g でしたか。
- 答え(2)
- 240 g
- 解き方(2)
- 蒸発させた水の量を□ g とすると、
10 % % 36 g g ( 600 – □ ) g
600 – □ = 36 ÷ 0.1 = 360
□ = 600 – 360 = 240 [g]
問7
A の容器には濃度が 6 % の食塩水が入っています。B の容器には濃度が分からない食塩水が入っています。A の食塩水 300 g と B の食塩水 150 g を混ぜると、8 % の食塩水ができることが分かっています。この 2 種類の食塩水を使い、濃度の違う食塩水を作ることにしました。
(1)B の食塩水の濃度は何 % ですか。
- 答え(1)
- 12 %
- 解き方(1)
- A と B を混ぜてできる 8 % の食塩水に入っている食塩の量は、
( 300 + 150 ) × 0.08 = 36 [g]
A の食塩水 300 g に入っている食塩の量は、
300 × 0.06 = 18 [g]
B の食塩水 150 g に入っている食塩の量は 36 – 18 = 18 [g] より、濃度は、
18 ÷ 150 × 100 = 12 [%]
(2)A の食塩水と B の食塩水を混ぜたところ、10 % の食塩水が 270 g できました。A の食塩水は何 g 入れましたか。
- 答え(2)
- 90 g
- 解き方(2)
- A を□ g いれたとすると、
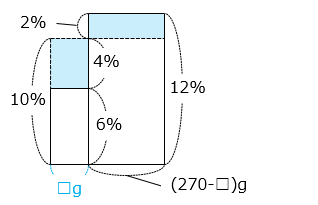
4 × □ = 2 × ( 270 – □ )
6 × □ = 540
□ = 90 [g]
(3)A の食塩水 300 g を用意しましたが、何 g かをこぼしてしまいました。300 g になるように水を加えたところ、5 % の食塩水が 300 g できました。このとき、こぼしてしまった A の食塩水は何 g ですか。
- 答え(3)
- 50 g
- 解き方(3)
- こぼしてしまったA を□ g とすると、
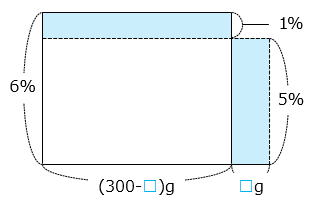
1 × ( 300 – □ ) = 5 × □
6 × □ = 300
□ = 50 [g]
(4)A の食塩水 300 g を用意しましたが、何 g かをこぼしてしまいました。300 g になるように B の食塩水を加えたところ、7.5 % の食塩水が 300 g できました。このとき、こぼしてしまった A の食塩水は何 g ですか。
- 答え(4)
- 75 g
- 解き方(4)
- こぼしてしまったA を□ g とすると、
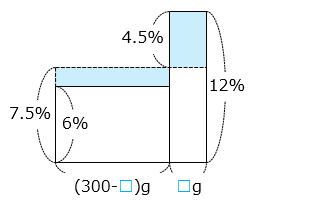
1.5 × ( 300 – □ ) = 4.5 × □
6 × □ = 450
□ = 75 [g]
