算数【基本】集合・ベン図
問1
(1)あるクラスの生徒30人に、プリンとコーヒーゼリーのそれぞれどちらが好きかどうかのアンケートを取りました。プリンを好きな生徒は11人、コーヒーゼリーを好きな生徒は15人で、そのうちどちらも好きな生徒は4人でした。
- アンケートの結果をベン図で表す
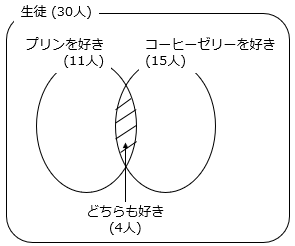
① プリンだけを好きな生徒は何人ですか。
- 答え(1)- ①
- 7人
- 解き方(1)- ①
- プリンだけを好きな生徒の人数 = プリンを好きな生徒の人数 – どちらも好きな生徒の人数 より、
11 – 4 = 7(人)
② どちらも好きでない生徒は何人ですか。
- 答え(1)- ②
- 8人
- 解き方(1)- ②
- どちらも好きでない生徒の人数は、
生徒の人数 – プリンまたはコーヒーゼリーを好きな生徒の人数
プリンまたはコーヒーゼリーを好きな生徒の人数は、
7 + 15 = 22(人)
よって、
30 – 22 = 8(人)
③ プリンまたはコーヒーゼリーのどちらか一方だけを好きな生徒は何人ですか。
- 答え(1)- ③
- 18人
- 解き方(1)- ③
- ①よりプリンだけを好きな生徒は7人。
コーヒーゼリーだけを好きな生徒は、15 – 4 = 11(人)
よって、どちらか一方だけを好きな生徒は、
7 + 11 = 18(人)
(2)生徒が40いるクラスで犬とねこのどちらを飼っているかを調査したところ、犬を飼っている人は14人、ねこを飼っている人は29人でした。
- 調査の結果をベン図で表す
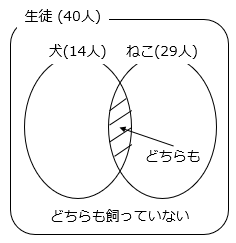
① 犬とねこをどちらも飼っている人は、最も少なくて何人ですか。
- 答え(2)- ①
- 3人
- 解き方(2)- ①
- どちらも飼っている人が最も少なくなるのは、どちらも飼っていない人が0人のとき。犬を飼っている人とねこを飼っている人の和が、生徒数より多い分がどちらも飼っている人になるので、
43 – 40 = 3(人)
② 犬とねこをどちらも飼っている人が12人のとき、犬とねこをどちらも飼っていない人は何人ですか。
- 答え(2)- ②
- 9人
- 解き方(2)- ②
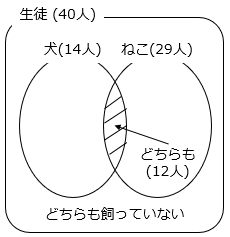
どちらも飼っていない人 = 生徒数 – 犬またはねこを飼っている人
犬またはねこを飼っている人 = ( 犬を飼っている人 + ねこを飼っている人 ) – どちらも飼っている人 より、
14 + 29 – 12 = 31(人)
よってどちらも飼っていない人は、
40 – 31 = 9(人)
(3)40人のクラスで、電車を使って通学している人は28人、バスを使って通学している人は16人、電車もバスも使っていない人は3人でした。電車とバスの両方を使っている人は何人ですか。
- 答え(3)
- 7人
- 解き方(3)
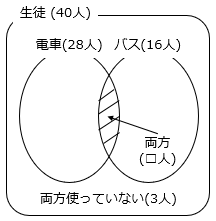
電車かバスを使って通学している人は、28 + 16 = 44(人)
電車もバスも使っていない人は3人なので、電車かバスを使っている人は、40 – 3 = 37(人)
よって、44 – 37 = 7(人)
(4)35人の学級で、兄と姉のいる人の人数を調べました。兄も姉もいる人は6人、兄も姉もいない人は8人で、兄だけがいる人は14人です。姉だけがいる人は何人ですか。
- 答え(4)
- 7人
- 解き方(4)
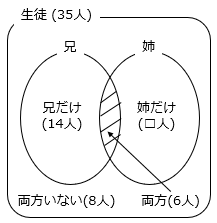
全生徒から、兄だけいる人、両方いる人、両方いない人を引けば、姉だけがいる人を求めることができる。
35 – 14 – 6 – 8 = 7(人)
(5)2けたの整数のうち、5で割り切れるが8で割り切れない整数はいくつありますか。
- 答え(5)
- 16個
- 解き方(5)
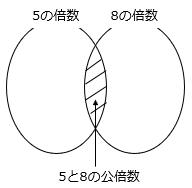
2けたの整数 = 10 ~ 99までの整数
5で割り切れるが8で割り切れない整数 = 5の倍数のうち、5と8の公倍数(40の倍数)でないもの
2けたの整数で5の倍数の個数を求める。
1~99までは、99 ÷ 5 = 19. … より19個
1~9までは、9 ÷ 5 = 1. … より1個
10~99までは、19 – 1 = 18(個)
2けたの整数で40の倍数の個数を求める。
1~99までは、99 ÷ 40 = 2. … より2個
よって、18 – 2 = 16(個)
(6)1から100までの整数の中で、3の倍数でも7の倍数でもない数は何個ありますか。
- 答え(6)
- 57個
- 解き方(6)
- 3の倍数は、100 ÷ 3 = 33. … より33個
7の倍数は、100 ÷ 7 = 14. … より14個
3と7の公倍数(21の倍数)は、100 ÷ 21 = 4. … より4個
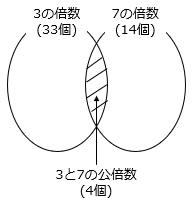
3または7の倍数は、
33 + 14 – 4 = 43(個)
3の倍数でも7の倍数でもない数は、
100 – 43 = 57(個)
問2
(1)ある学年で国語と算数のテストをしました。国語のテストで70点以上をとった生徒は学年全体の \(\dfrac{4}{5}\) でした。算数のテストで70点以上をとった生徒は学年全体の \(\dfrac{2}{3}\) でした。両方のテストで70点以上をとった生徒は学年全体の \(\dfrac{5}{9}\) でした。両方のテストとも70点未満だった生徒は36人でした。
① 学年全体の人数を□人とするとき、国語だけ70点以上だった生徒は何人ですか。□を使った式で表しなさい。
- 答え(1)- ①
- \(\dfrac{11}{45}\) × □
- 解き方(1)- ①
- テストの結果をベン図で表す。
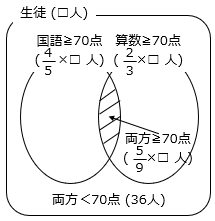
国語だけ70点以上だった人数 = 国語が70点以上の人数 – 両方70点以上の人数 より、
\(\dfrac{4}{5}\) × □ – \(\dfrac{5}{9}\) × □
= ( \(\dfrac{4}{5}\) – \(\dfrac{5}{9}\) ) × □ = \(\dfrac{11}{45}\) × □(人)
② 学年全体の人数を求めなさい。
- 答え(1)- ②
- 405人
- 解き方(1)- ②
- 少なくとも一方が70点以上だった人数を□を使ってあらわすと、
\(\dfrac{11}{45}\) × □ + \(\dfrac{2}{3}\) × □
= ( \(\dfrac{11}{45}\) + \(\dfrac{2}{3}\) ) × □ = \(\dfrac{41}{45}\) × □(人)
両方とも70点未満の人数は、
□ – \(\dfrac{41}{45}\) × □ = \(\dfrac{4}{45}\) × □(人)
と表すことができる。よって、
\(\dfrac{4}{45}\) × □ = 36
□ = 36 × \(\dfrac{45}{4}\) = 405(人)
③ 国語だけ70点以上だった生徒の人数と、算数だけ70点以上だった生徒の人数を比べると、どちらが何人多かったですか。
- 答え(1)- ③
- 国語が54人
- 解き方(1)- ③
- ①②より、国語だけ70点以上だった生徒の人数は、
\(\dfrac{11}{45}\) × 405 = 99(人)
算数だけ70点以上だった生徒の人数は、
( \(\dfrac{2}{3}\) – \(\dfrac{5}{9}\) ) × 405
= \(\dfrac{1}{9}\) × 405 = 45(人)
したがって、国語が 99 – 45 = 54(人) 多かった。
(2)40人のクラスで算数と国語のテストをしました。国語が80点以上の人は22人、算数が80点以上の人は15人でした。クラスの30%の人が、国語と算数の両方とも80点以上のとき、両方とも80点未満の人は何人ですか。
- 答え(2)
- 15人
- 解き方(2)
- 両方とも80点以上の人は、40 × 0.3 = 12(人)
テストの結果をベン図で表す。
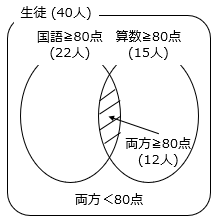
少なくとも一方が80点以上の人は、
22 + 15 – 12 = 25(人)
よって、両方とも80点未満の人は、
40 – 25 = 15(人)
(3)ある学校の生徒300人について、そろばんと水泳を習っている人数を調べました。そろばんを習っている生徒は全体の25%、水泳を習っている生徒は全体の30%、そろばんも水泳も習っていない生徒は全体の60%でした。そろばんも水泳も習っている生徒は何人ですか。
- 答え(3)
- 45人
- 解き方(3)
- そろばんを習っている生徒は 300 × 0.25 = 75(人)
水泳を習っている生徒は 300 × 0.3 = 90(人)
両方とも習っていない生徒は 300 × 0.6 = 180(人) より、少なくとも一方を習っている生徒は 300 – 180 = 120(人) である。
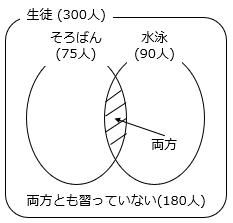
両方習っている生徒の人数は、
75 + 90 – 120 = 45(人)
問3
A、B、C、D、E の5人の生徒うち、3人は運動部(野球部またはサッカー部)に入り、2人は文化部に入っていて、次の①~④のことがわかっています。
① A、C、D は3人とも異なる部に入っています。
② B、D、E は3人とも異なる部に入っています。
③ 運動部に入っていないのは、C、E です。
④ 野球部には2名の生徒が入っています。
このとき、サッカー部に入っているのはどの生徒ですか。
- 答え
- D
- 解き方
- ③より、C、E は文化部である。すなわち、運動部に入っているのは、A、B、D の3人。
①②より、D は A、B の2人とは異なる部に入っている。
よって、サッカー部に入っているのは D。










