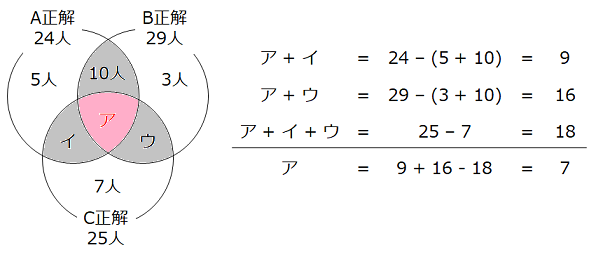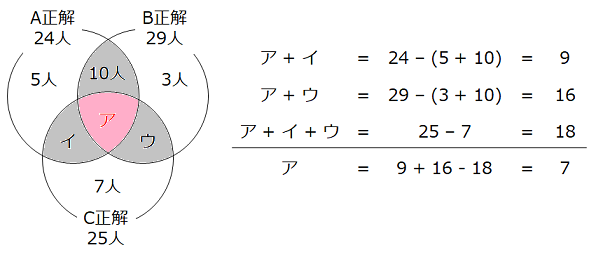算数【入試】集合・ベン図

問１

1以上1000以下の整数について、次の(1)、(2)の問いに答えなさい。

(1) 2でも5でも割り切れない整数の個数を求めなさい。

(2) 2でも5でも7でも割り切れない整数を求めなさい。

答え(1)

400個

答え(2)

343個

問２

生徒全員に試験Aと試験Bを行ったところ、以下の①から④までの結果がわかりました。

①試験Aが80点以上だった人の数は、全体の\(\dfrac{2}{5}\)でした。

②試験Bが80点以上だった人の数は、全体の\(\dfrac{1}{3}\)でした。

③試験A、Bともに80点以上だった人の数は、26人でした。

④試験Bが80点未満の人の数が70人以上であれば、試験Bのみ再試験が行われる予定でしたが、再試験は行われませんでした。

このとき次の問いに答えなさい。

(1) 生徒の人数は何人ですか。

(2) 1ヶ月後にもう一度、生徒全員に試験Aと試験Bを行ったところ、試験A、Bともに80点未満だった人の数は、前回に比べて22人減りました。また、試験A、Bともに80点以上だった人の数は変わらず26人でしたが、試験Aが80点以上だった人の数と試験Bが80点以上だった人の数の比は6 : 5になりました。このとき、試験Aが80点未満だった人は何人ですか。

答え(1)

90人

答え(2)

42人

解き方(1)

生徒全員の人数を⑮とすると、試験Aが80点以上だった人数は⑥、試験Bが80点以上だった人数は⑤となる。

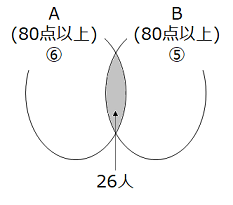
試験A、Bともに80点以上だった人数が26人であったことから、⑥ > 26かつ、⑤ >= 26、すなわち① > 5となる。また、試験Bが80点未満の人数が70人未満であったことから、⑮ – ⑤ < 70、すなわち① < 7となる。よって、① = 6となり、生徒の人数は15 × 6 = 90(人)

解き方(2)

試験Aが80点以上だった人数を⑥とすると、試験Bが80点以上だった人数は⑤となる。前回、試験A、Bともに80点未満だった人数は、90 – 36 – 30 + 26 = 50(人)なので、今回は50 – 22 = 28(人)となる。

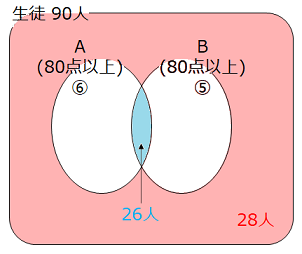
よって、90 – ⑥ – ⑤ + 26 = 28
① = 8
したがって、試験Aが80点未満だった人数は、90 – 48 =42(人)

問３

170人の生徒が2問のテストを受けました。1番を正解した人の\(\dfrac{3}{8}\)は2番も正解し、2番を正解した人の\(\dfrac{1}{4}\)は1番も正解しました。両方とも正解しなかった人は17人でした。1番だけ正解した人は何人ですか。

答え

45人

解き方

1番だけ正解した人、両方とも正解した人、2番だけ正解した人の比は5 : 3 : 9となる。それぞれの人数を⑤、③、⑨とすると、

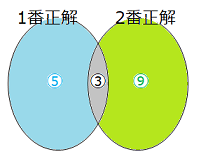
⑤ + ③ + ⑨ = 170 – 17
① = 9
よって、1番だけ正解した人は、5 × 9 = 45(人)

問４

ある中学校の男子生徒と女子生徒の割合は4 : 5で、自転車通学の生徒と徒歩通学の生徒の割合は5 : 7です。男子で自転車通学の生徒が70人、女子で徒歩通学の生徒が115人でした。この学校の全校生徒は何人ですか。ただし、通学方法は自転車と徒歩のみとします。

答え

324人

解き方

全校生徒の人数を㊱とすると、各人数は以下の表のようになる。

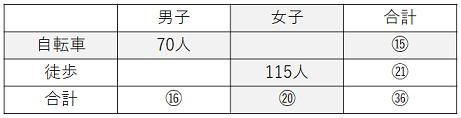
女子で自転車通学の生徒は、⑮ – 70となる。女子の生徒数に着目すると、
⑳ = ⑮ – 70 + 115
① = 9
よって、全校生徒は36 × 9 = 324(人)

問５

60人の生徒が問題A、B、Cの3問からなるテストを受けました。問題Aを正解した人は24人、問題Bを正解した人は29人、問題Cを正解した人は25人、問題Aだけを正解した人は5人、問題Bだけを正解した人は3人、問題Cだけを正解した人は7人、問題AとBを正解してCを正解できなかった人は10人でした。このとき、3問すべてを正解した人は何人ですか。

答え

7人

解き方