算数【基本】旅人算

旅人算とは

旅人算とは、2つのものが、追いついたり出会ったりするまでの時間や道のりを求める問題である。
●進行方向が同じ（追いつき算）
追いつく時間 = 2つのものの間の距離 ÷ 2つのものの速さの差
●進行方向が反対（出会い算）
出会う時間 = 2つのものの間の距離 ÷ 2つのものの速さの和

問１

（１）Aさんは学校から1530m離れた駅に分速70mで歩いて向かいます。Bさんは駅から学校へ分速100mでAさんと同時に向かいます。2人が出会うのは出発してから何分後ですか。

答え（１）

9分後

解き方（１）

1530 ÷ ( 70 + 100 ) = 1530 ÷ 170 = 9(分後)

（２）A君は分速60mの速さで駅に向かいました。忘れ物に気づいた母が、A君が家を出てから7分後に、自転車でA君を追いかけました。自転車の速さは分速200mです。母がA君に追いつくのは、A君が家を出発してから何分後ですか。

答え（２）

10分後

解き方（２）

A君は家を出てから7分後、家から 60 × 7 = 420(m)の地点にいます。母がA君に追いつくのにかかる時間は、
420 ÷ ( 200 – 60 ) = 420 ÷ 140 = 3(分)
よって、A君が出発してから 7 + 3 = 10(分後)

（３）1周6kmの公園のまわりをAさんは毎分240mの速さで、Bさんは毎分150mの速さで同じ向きに走ることにしました。Aさんが出発してから10分後にBさんが同じ地点を出発したとき、Aさんが初めてBさんに追いつくのは、Bさんが出発してから何分後ですか。

答え（３）

40分後

解き方（３）

10分間でAさんが進む距離は 240 × 10 = 2400(m)
このとき、AさんとBさんの距離は 6 × 1000 – 2400 = 3600(m)

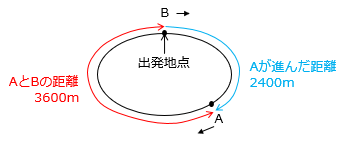
よって、AさんがBさんに追いつくのは、
3600 ÷ ( 240 – 150 ) = 3600 ÷ 90 = 40(分後)

（４）池の周りをAさんは12分、Bさんは18分で1周します。2人が同時に同じ地点から反対方向に進むと、出会うのは何分何秒後ですか。

答え（４）

7分12秒後

解き方（４）

AさんとBさんの速度の比は、\(\dfrac{1}{12}\)：\(\dfrac{1}{18}\) = 3：2
池の距離を5とすると、Aは3、Bは2進んだところで出会う。
よって、Aは12分のうち\(\dfrac{3}{5}\)進んだところとなり、
12 × \(\dfrac{3}{5}\) = 7.2(分)
= 7分12秒

【別解】
池のまわりの距離を□mとすると、Aさんの速度は \(\dfrac{□}{12}\)(m/分)、Bさんの速度は \(\dfrac{□}{18}\)(m/分) とあらわすことができる。
よって2人が出会うのは、
□ ÷ ( \(\dfrac{□}{12}\) + \(\dfrac{□}{18}\) )
= □ ÷ ( \(\dfrac{3\ ×\ □\ +\ 2\ ×\ □}{36}\) )
= □ ÷ \(\dfrac{5\ ×\ □}{36}\)
= □ × \(\dfrac{36}{5\ ×\ □}\)
= \(\dfrac{36}{5}\)
= 7.2(分後)

（５）学校から公園に向かって、A君は15時30分、B君は15時35分に出発しました。A君は分速80m、B君は分速120mで歩きます。B君はA君に何時何分に追いつきますか。

答え（５）

15時45分

解き方（５）

B君が学校を出発したとき、A君は学校から 80 × 5 = 400(m)のところにいる。
よって、B君が出発してからA君に追いつくのは、
400 ÷ ( 120 – 80 ) = 10(分後)
したがって、15時45分

（６）1.8km離れた2地点A、Bがあります。兄と弟は地点Aを同時に出発し、AとBの間を何回か往復します。兄は分速100m、弟は分速60mで進みます。

① 2人が初めてすれ違うのは、地点Aを出発してから何分何秒後ですか。

答え（６）- ①

22分30秒後

解き方（６）- ①

兄が初めにB地点に到着するのは、出発してから 1.8 × 1000 ÷ 100 = 18(分後)。
このとき、弟はA地点から 60 × 18 = 1080(m)の地点にいる。

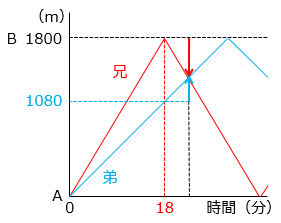
2人が初めてすれ違うのは、兄がB地点に到着してから
( 1800 – 1080 ) ÷ ( 100 + 60 ) = 4.5(分後)
よってA地点を出発してから 18 + 4.5 = 22.5 = 22分30秒後

② 2人が初めて同時に地点Aに戻るのは、兄が何回目に地点Aに戻ったときですか。

答え（６）- ②

5回目

解き方（６）- ②

兄がAB間を往復するのにかかる時間は 18 × 2 = 36(分)
弟がAB間を往復するのにかかる時間は ( 1800 ÷ 60 ) × 2 = 60(分)
2人が初めて同時に地点Aに戻るのは、兄と弟がそれぞれAB間を往復するのにかかる時間の最小公倍数のときなので、180分後
よって、180 ÷ 36 = 5(回目)

（７）1周900mの池のまわりをAさんとBさんが歩きます。AさんはBさんよりも分速30mはやく歩くことができます。2人が同時に同じ場所から同じ方向に歩くと、AさんがBさんに初めて追いつくのに2周半かかりました。

① 2人が歩き始めてから何分後にAさんはBさんに追いつきますか。

答え（７）- ①

30分後

解き方（７）- ①

スタート地点において、AさんとBさんの距離は池1周分の900mと考えられるので、
900 ÷ 30 = 30(分後)

② Aさんは分速何mで歩きますか。

答え（７）- ②

分速75m

解き方（７）- ②

AさんがBさんに追いつくまでに歩いた距離は 900 × 2.5 = 2250(m)、①よりかかった時間は30分より、
2250 ÷ 30 = 75(m/分)

（８）Aさんは学校から家まで分速50mで30分間歩いて帰ります。ある日、Aさんは4時に学校を出て家に向かって歩いていました。学校を出てから3分後に雨が降り始めたので分速75mで走りました。お母さんは4時5分に家を出て分速125mで学校へ向かったところ、途中でAさんと出会いました。

① 学校から家までの道のりは何mですか。

答え（８）- ①

1500m

解き方（８）- ①

50 × 30 = 1500(m)

② Aさんとお母さんが出会ったのは、何時何分ですか。

答え（８）- ②

4時11分

解き方（８）- ②

4時5分、Aさんが学校から進んだ距離は、
50 × 3 + 75 × 2 = 150 + 150 = 300(m)
よってお母さんとの距離は 1500 – 300 = 1200(m)
2人が出会ったのは、お母さんが家を出てから、
1200 ÷ ( 75 + 125 )
= 6(分後)
よって、4時11分

（９）公園の周りを、A君は毎分220mの速さで時計回りに、B君は毎分280mの速さで反対回りに走ります。2人は同じ位置から同時に出発して、60分間走ります。最初にすれ違ったのは、出発してから6分36秒でした。

① 2回目にすれ違うのは、出発してから何分何秒後ですか。

答え（９）- ①

13分12秒後

解き方（９）- ①

2回目にすれ違うのは最初にすれ違ってから、6分36秒後なので、13分12秒後

② 公園の周りは1周何mですか。

答え（９）- ②

3300m

解き方（９）- ②

6分36秒 = \(\dfrac{33}{5}\) (分) より、
( 220 + 280 ) × \(\dfrac{33}{5}\)
= 500 × \(\dfrac{33}{5}\)
= 3300(m)

③ 60分間に2人は何回すれ違いますか。

答え（９）- ③

9回

解き方（９）- ③

2人がすれ違うのは、6分36秒(= \(\dfrac{33}{5}\) (分))ごとなので、
60 ÷ \(\dfrac{33}{5}\)
= 60 × \(\dfrac{5}{33}\)
= \(9\dfrac{1}{11}\)
よって、9回

（１０）姉妹が図書館へ行きます。妹は家を先に出て歩いて図書館に向かい、姉は後から自転車で追いかけ、妹を追いこし、先に図書館に着きました。グラフは妹が家を出発してからの姉妹の距離を表しています。

① 妹の歩く速さは分速何mですか。

答え（１０）- ①

分速50m

解き方（１０）- ①

姉との距離が大きくなり続けている15分までは、姉は家を出発していない。
よって、姉との距離は妹が進んだ距離と等しい。
750 ÷ 15 = 50(m/分)

② 姉の速さは分速何mですか。

答え（１０）- ②

分速200m

解き方（１０）- ②

グラフより、姉が出発したとき妹との距離は750mである。そして妹に追いつくまでの時間は 20 – 15 = 5(分) である。
姉と妹の速さの差は、
750 ÷ 5 = 150(m/分)
よって、姉の速さは 50 + 150 = 200(m/分)

③ 妹は家から何分で図書館に着きましたか。

答え（１０）- ③

32分

解き方（１０）- ③

グラフより、姉が図書館に着いたのは、家を出発してから 23 – 15 = 8(分後)
よって家と図書館の距離は 200 × 8 = 1600(m)
妹が図書館までにかかる時間は、
1600 ÷ 50 = 32(分)

問２

（１）グラフは7時30分から10時の間にP駅とQ駅の間を走る1台のバスの様子をあらわしたものです。P駅から9kmはなれたQ駅までは10分かかり、バスは駅に到着してから10分後に出発します。

① バスの速さは分速何mですか。

答え（１）- ①

分速900m

解き方（１）- ①

バスは9kmの道のりを10分で移動するので、
9 × 1000 ÷ 10 = 900(m/分)

② A君は7時50分にP駅を出発し、分速100mの速さで、バスが通る道を使ってQ駅に向かいました。A君がバスと出会うのは何回ですか。

答え（１）- ②

5回

解き方（１）- ②

A君がQ駅に到着するのは 9000 ÷ 100 = 90(分後) の9時20分。A君の移動の様子をグラフに書き込むと、

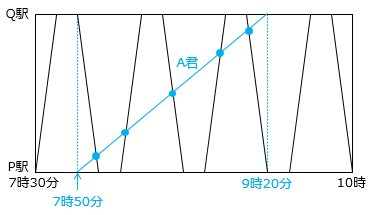
A君がバスと出会うのは5回

③ ②のとき、バスがA君を初めて追いこすのは、P駅から何mのところですか。

答え（１）- ③

2250m

解き方（１）- ③

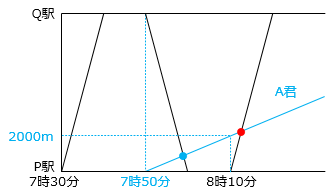
バスがA君を追いこすのは、バスがP駅からQ駅に向かうとき。
バスがP駅を8時10分に出発するとき、A君はP駅から、
100(m/分) × 20(分) = 2000(m)の位置にいる。
2000 ÷ ( 900 – 100 ) = 2.5(分)
8時10分の2.5分後にバスがA君を追いこす。このとき、P駅からの距離は、
100 × 22.5 = 2250(m)

（２）Aくんは甲町から乙町に向かって分速80mの速さで歩き、ちょうど同じ時間にBくんが乙町から甲町に向かって分速60mの速さで歩き始めました。2人は歩き始めて20分後に出会いました。甲町から乙町までの距離は何kmですか。

答え（２）

2.8km

解き方（２）

Aくんが歩いた距離は 80 × 20 = 1600(m)
Bくんが歩いた距離は 60 × 20 = 1200(m)
よって甲町から乙町の距離は、
1600 + 1200 = 2800(m) = 2.8(km)

（３）兄と弟は同時に家を出発し、公園へ向かいました。兄は毎分75mの速さで歩きましたが、途中のコンビニで買い物をし、その後再び同じ速さで歩き始めました。弟は毎分50mの速さで歩き、コンビニで兄を追いこしましたが、追いこしてから12分30秒後に兄に追いこされました。兄が再び歩き始めたのは、弟に追いこされてから何分何秒後ですか。

答え（３）

4分10秒後

解き方（３）

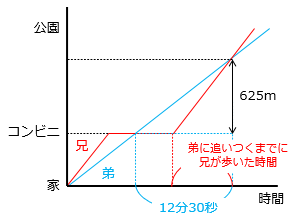
弟が12分30秒(=\(12\dfrac{1}{2}\))間で歩いた距離は、50 × \(12\dfrac{1}{2}\) = 625(m)
兄と弟は同じ距離歩いており、兄が歩いた時間は、625(m) ÷ 75(m/分) = \(8\dfrac{1}{3}\)(分)となる。
\(12\dfrac{1}{2}\)分中 \(8\dfrac{1}{3}\) が兄が歩いていた時間なので、
\(12\dfrac{1}{2}\) – \(8\dfrac{1}{3}\)
= \(4\dfrac{1}{6}\)
= 4分10秒後

（４）Aさんはハガキを投函するために、家から1200m離れた郵便局へ行きます。また、BさんはAさんが家を出発するのと同時に郵便局を出発し、Aさんの家に向かいます。2人は出発してから5分後にすれ違いました。Aさんは郵便局でハガキを投函するとすぐに家に戻ります。Aさんの行きと帰りの速さの比は 5：2、Bさんの歩く速さは分速40mです。グラフは、そのときのAさんとBさんの様子を表したものです。

① Aさんが郵便局に着くまでの速さは分速何mですか。

答え（４）- ①

分速200m

解き方（４）- ①

1200(m) ÷ 5(分) = 240(m/分)・・・AさんとBさんの速度の和
240 – 40 = 200

【別解】
Aさんが郵便局に着くまでの速さを分速□mとすると、
( □ + 40 ) × 5 = 1200
□ + 40 = 240
□ = 240 – 40 = 200(m/分)

② AさんがBさんを追いこしたのは、Aさんが郵便局を出てから何分後ですか。

答え（４）- ②

6分後

解き方（４）- ②

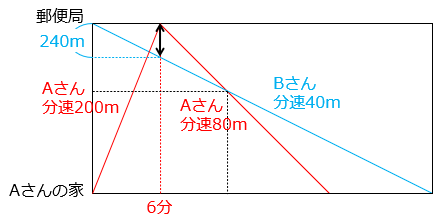
Aさんが郵便局に着いたのは、出発してから 1200 ÷ 200 = 6(分後)
Aさんが家に戻るときの速さは 200 × \(\dfrac{2}{5}\) = 80(m/分)
Aさんが郵便局を出るとき、BさんはAさんから、
40(m/分) × 6(分) = 240(m)のところにいる。
よって、240 ÷ ( 80 – 40 ) = 6(分後)

（５）図のように3つの地点P、Q、Rがあり、それらを結ぶ道があります。地点PとQ、地点QとRを結ぶ道は坂道、地点PとRは平らな道です。

　Aさんは8時に自転車でP地点を出発し、P → Q → R → P の順に、上り坂 → 下り坂 → 平らな道を通って走ります。Bさんは8時30分に自転車でP地点を出発し、P → R → Q → P の順に、平らな道 → 上り坂 → 下り坂を通って走ります。平らな道をAさんは時速10km、Bさんは時速15kmで走ります。2人とも上り坂を走るときの速さは、平らな道を走るときに比べて2割減になり、下り坂を走るときの速さは、平らな道を走るときに比べて2割増しになります。

　このとき、AさんとBさんが出会うのは何時何分ですか。

答え（５）

9時20分

解き方（５）

Aさんの上りの速さは 10 × 0.8 = 8(km/時)
よって、Aさんが地点Qに着くのは 8 ÷ 8 = 1(時間後) の9時。
一方、Bさんが地点Rに着くのは 10 ÷ 15 = \(\dfrac{2}{3}\)(時間後) = 40(分後) の9時10分。
9時10分のときのAさんの位置を求める。
Aさんの下りの速さは 10 × 1.2 = 12(km/時)より、地点QからRに向かって 12 × \(\dfrac{10}{60}\) = 2(km) の地点にいる。

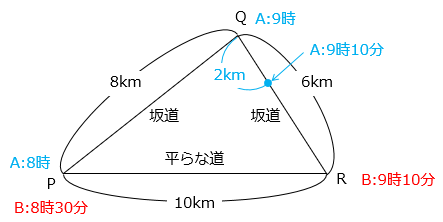
Bさんの上りの速さは 15 × 0.8 = 12(km/時)。
2人が出会うのは9時10分から、
4 ÷ ( 12 + 12 ) = \(\dfrac{1}{6}\)(時間後) = 10(分後)
よって、9時20分

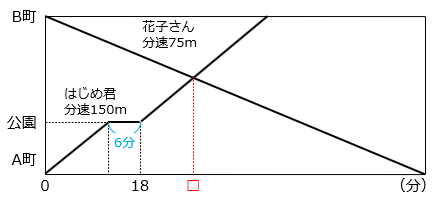
（６）A町とB町は5.4km離れています。9時にはじめ君はA町からB町に向けて出発し、花子さんはB町からA町に向けて出発しました。はじめ君は途中とちゅうにある公園で6分間休みました。図は、はじめ君と花子さんが出発してからの時間と道のりの関係を表しています。はじめ君の進む速さは分速150m、花子さんの進む速さは分速75mで、それぞれ一定とします。

2人が出会うのは何時何分ですか。

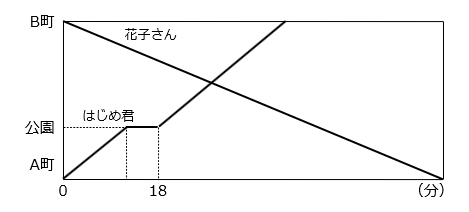
答え（６）

9時28分

解き方（６）

9時18分時点のはじめ君と花子さんの距離を求める。
はじめ君は6分間休んだので進んだ時間は12分である。
はじめ君の進んだ距離は、150(m/分) × 12(分) = 1800(m)となる。
一方、花子さんは9時18分時点で進んだ距離は、
75(m/分) × 18(分) = 1350(m)
9時18分時点でのはじめ君と花子さんの距離は、
5.4(km) – 1800(m) – 1350(m) = 2250(m)
よって、2250 ÷ ( 150 + 75 ) = 10(分)
9時18分から10分後に出会う。したがって、9時28分。

【別解１】
はじめ君は途中に6分休んだので、出発した時間を9時6分とみなす。
9時6分時点に花子さんは、75(m/分) × 6(分) = 450(m)の距離進んでいる。
9時6分時点のはじめ君と花子さんの距離は、5.4(km) – 450(m) = 4950(m)。
よって、4950 ÷ ( 150 + 75 ) = 22(分)後に出会う。
9時6分から22分後に出会う。したがって、9時28分。

【別解２】

2人が出会うのを□分後とする。
はじめ君が進んだ距離と、花子さんが進んだ距離の和が5.4kmなので、
150 × ( □ – 6 ) + 75 × □ = 5.4 × 1000
150 × □ – 900 + 75 × □ = 5400
225 × □ = 5400 + 900 = 6300
□ = 28(分後)
よって、9時28分

（７）兄と弟は家から3900m離れた公園までを走って往復しました。弟が家を出発して3分後に兄は家を出発しました。兄は分速260m、弟は分速130mで走りました。グラフは、弟が家を出発してからの時間と、2人の家からの道のりを表したものです。

① 兄が弟に追いついたのは、家から何mのところですか。

答え（７）- ①

780m

解き方（７）- ①

兄が家を出発したとき、弟が進んだ距離は、
130(m/分) × 3(分) = 390(m)
よって、390 ÷ ( 260 – 130 ) = 3(分)後に出会う。
260 × 3 = 780(m)

【別解】

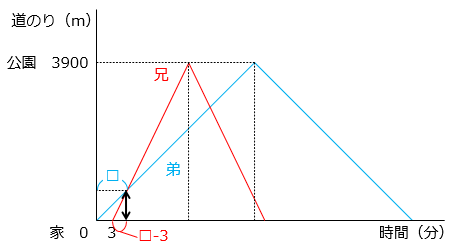
兄は弟が家を出発してから□分後に弟に追いついたとする。このとき、兄と弟が進んだ道のりは等しいので、
260 × ( □ – 3 ) = 130 × □
260 × □ – 780 = 130 × □
260 × □ – 130 × □ = 780
130 × □ = 780
□ = 6(分後)
6分間で弟が進んだ道のりは 130 × 6 = 780(m)

② 弟が公園に到着するのは、兄が公園に到着してから何分後ですか。

答え（７）- ②

12分後

解き方（７）- ②

兄が公園に到着するのは、弟が家を出てから、
3 + 3900 ÷ 260 = 3 + 15 = 18(分後)
弟が公園に到着するのは、弟が家を出てから、
3900 ÷ 130 = 30(分後)
よって、30 – 18 = 12(分後)

③ 2人が2回目に会ったのは、弟が家を出発してから何分後ですか。

答え（７）- ③

22分後

解き方（７）- ③

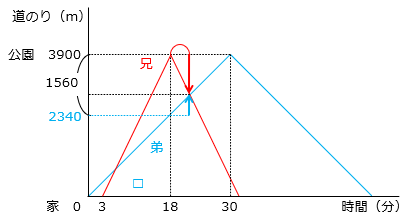
兄が公園に到着して家に向かう時間は、弟が出発して18分後。
弟が18分で進む距離は、130(m/分) × 18(分) = 2340(m)
このときの兄との距離は、3900 – 2340 = 1560(m)となり、
1560 ÷ ( 260 + 130 ) = 4(分)後に出会う。よって、18 + 4 = 22(分後)

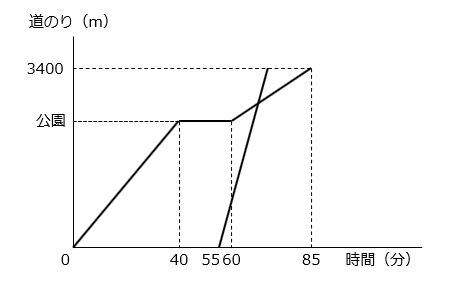
（８）Aさんは家から3400m離れた映画館まで歩いて行きました。Aさんは途中公園で20分休み、家を出てから85分後に映画館に着きました。公園までは分速60mで歩き、公園で休んだ後は分速40mで歩きました。Aさんが家を出てから55分後にお兄さんが自転車で家を出発し、Aさんと同じ道を追いかけました。自転車の速さは分速200mです。グラフは、Aさんとお兄さんが映画館に着くまでの道のりを表したものです。お兄さんがAさんに追いつくのは、Aさんが家を出てから何分後ですか。

答え（８）

70分後

解き方（８）

60分時点でのAさんとお兄さんの距離を求める。
Aさんは40分の距離を歩いているので、60 × 40 = 2400(m)進んでいる。
お兄さんは5分の距離進んでいるので、200 × 5 = 1000(m)
２人の距離は、2400 – 1000 = 1400(m)
よって、1400 ÷ ( 200 – 60 ) = 10(分)後に出会う。
60分の10分後に出会うので70分後。

【別解】

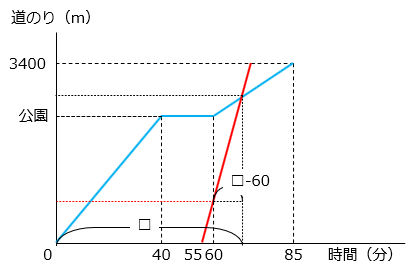
お兄さんがAさんに追いつくのは、Aさんが家を出てから□分後とする。
２人の距離は 2400 – 1000 = 1400(m)
式であらわすと、
1400 ÷ ( 200 – 60 ) = □ – 60
1400 ÷ 140 = □ – 60
10 = □ – 60
□ = 10 + 60 = 70(分後)

（９）Aさんは、午後3時30分に自宅からのむかえの車が学校について、すぐ帰宅することにしています。ある日、Aさんは、学校が早く終わったので、午後3時ちょうどに学校を出発してそのままむかえの車が来る道を自宅へむかって歩いて帰りました。その帰り道の途中でむかえの車と出会い、車に乗って自宅に帰ったところ、いつもより6分早く帰宅することができました。Aさんがむかえの車と出会った時刻は午後3時何分ですか。

　ただし、Aさんは一定の速さで歩き、車も一定の速さで走ります。

答え（９）

27分

解き方（９）

ある日の様子をグラフで表すと、

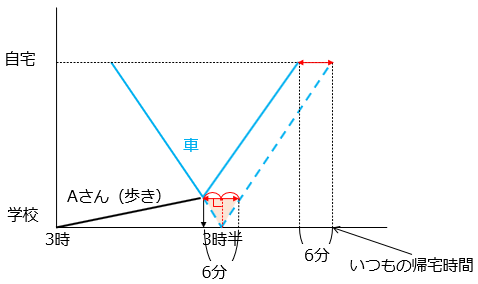
グラフの▲部分は2等辺三角形になっている。
よって、Aさんがむかえの車と出会った時刻は午後3時27分