問1
A町とB町をむすぶ道があります。太郎君は午前8時30分に分速100mでA町を、次郎君は太郎君の30分後に分速120mでA町をそれぞれ出発してB町に向かいました。三郎君は太郎君の1時間後に分速60mでB町を出発しA町に向かいました。3人は道の途中でちょうど出会いました。
(1) 3人が出会ったのは、何時何分ですか。
(2) A町とB町は何km離れていますか。
- 答え(1)
- 11時30分
- 答え(2)
- 25.2km
- 解き方(1)
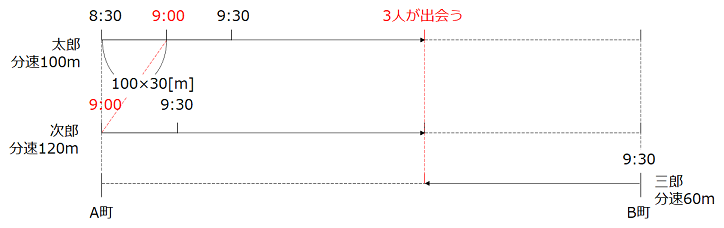
次郎君がA町を出発するとき、太郎君は3000m先にいる。太郎君と次郎君の速度差は120 – 100 = 20なので、2人が出会うのは3000 ÷ 20 = 150(分後)
よって、11時30分。
- 解き方(2)
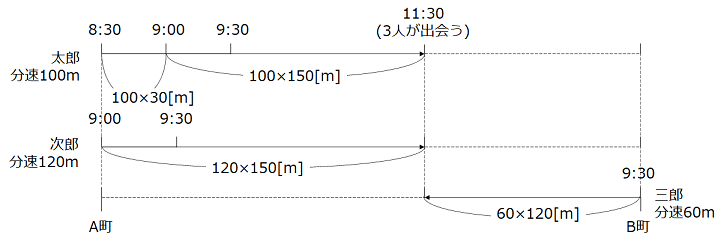
3000 + 15000 + 7200 = 25200[m]、すなわち25.2km
問2
A君、B君、C君の3人は、学校から目的地まで同じ道を歩きました。A君は学校を8時に出発し、B君は10分遅れて、C君はさらに10分遅れて出発しました。A君は、B君に8時40分に追いこされ、C君に8時55分に追いこされました。
(1) B君とC君の速さの比を求めなさい。
(2) 目的地にはB君とC君が同時につきました。B君とC君が目的地に着いたのは何時何分ですか。
(3) B君とC君が目的地に到着したとき、A君は目的地まであと900mの地点にいました。学校から目的地までの道のりは何mですか。
- 答え(1)
- 28 : 33
- 答え(2)
- 9時16分
- 答え(3)
- 6600m
- 解き方(1)
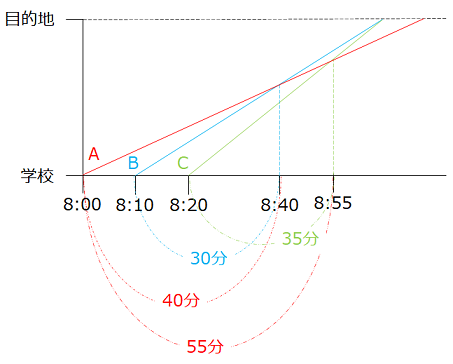
A君の速さを1とすると、B君の速さは\(\dfrac{40}{30}\)、C君の速さは\(\dfrac{55}{35}\)となる。\(\dfrac{40}{30}\) : \(\dfrac{55}{35}\) = 28 : 33
- 解き方(2)
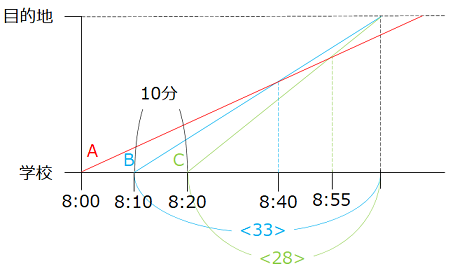
(1)より、B君が目的地に到着するのにかかった時間を<33>とすると、C君が目的地に到着するのにかかった時間は<28>となる。その差は10分なので、
<33> – <28> =10
<1> = 2(分)
よって、B君が出発してから目的地に到着したのは、<33> = 66(分後)
すなわち、9時16分
- 解き方(3)
- B君が目的地に到着するのにかかった時間を<33>とすると、A君が目的地に到着するのにかかった時間は<44> = 88(分)となり((2)より)、9時28分。
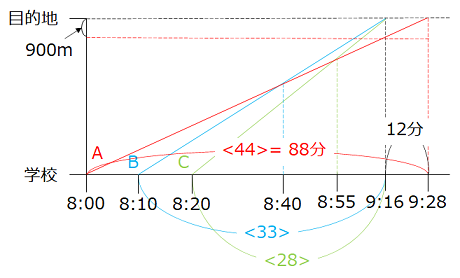
B君、C君が目的地に着いてから12分後であり、その間に進んだ道のりは900mである。学校から目的地までの道のりは、
\(\dfrac{900}{12}\) × 88 = 6600(m)
問3
1周600mのコースがあります。A君とB君は、同じ場所から同時に同じ方向に走りだしました。A君は毎分120mで5周、B君は毎分80mで4周走りました。
(1) どちらが何分早く走り終えましたか。
(2) C君は2人より8分遅れて同じ場所を出発し、2人とは反対方向に毎分60mで走りました。C君は初めてA君と出会ってから何分何秒後にB君と出会いましたか。
- 答え(1)
- A君が5分
- 答え(2)
- 2分40秒後
- 解き方(1)
- A君が走り終わるのにかかった時間は\(\dfrac{600\times5}{120}\) = 25(分)、B君が走り終わるのにかかった時間は\(\dfrac{600\times4}{80}\) = 30(分)。よって、A君が5分早く走り終えた。
- 解き方(2)
- C君が出発したとき、A君は120 × 8 = 960(m)走っているため、スタート地点から360m進んだところにいる。同様に、このときB君は80 × 8 = 640(m)走っているため、スタート地点から40m進んだところにいる。C君が出発してからA君と出会うのは、\(\dfrac{600-360}{120+60}\) = \(1\dfrac{1}{3}\) = 1分20秒後。C君が出発してからB君と出会うのは、\(\dfrac{600-40}{80+60}\) = 4分後。
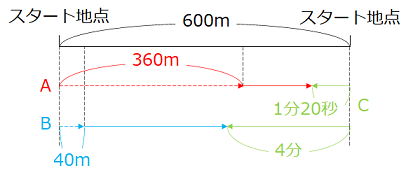
よって、B君に出会ったのはA君と出会ってから2分40秒後。
問4
太郎君はバスに乗るために停留所Aに行くと、21分待たなければなりませんでした。そこで、次の停留所Bまで分速80mの速さで歩いて行くと、歩き始めてから24分後にバスに追いこされました。さらに16分歩いて停留所Bに着き、2分待つと次のバスが来ました。(2台のバスは同じ速さで走り、バスが停留所に止まっている時間は考えないものとします)
(1) バスの速さは時速何kmですか。
(2) 2番目のバスが停留所Aを出発したのは、1番目のバスが停留所Aを出発してから何分後ですか。
- 答え(1)
- 時速38.4km
- 答え(2)
- 16分後
- 解き方(1)
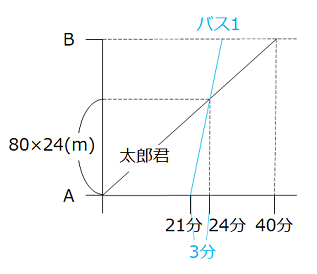
\(\dfrac{80\times24}{3}\) = 分速640m = 時速38.4km
- 解き方(2)
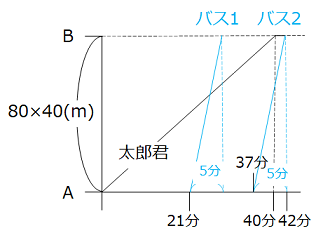
バスが停留所AからBに着くまでにかかる時間は、\(\dfrac{80\times40}{640}\) = 5(分)である。2番目のバスが停留所Bに着くのは太郎君が出発してから42分後なので、出発したのは、37分後となる。よって、1番目のバスが出発してから16分後となる。
問5
A地点からB地点に向かって時速36kmのタクシーに乗り、太郎君が出発しました。同時に次郎君は時速3.6kmで、同じ道をA地点からB地点に向けて歩いて出発しました。タクシーは太郎君をB地点で降ろすと、引き返して途中まで来ていた次郎君を乗せてB地点に向かいました。次郎君は太郎君がB地点に着いてから1時間後にB地点に着きました。(タクシーの乗り降りにかかる時間は考えないものとします。)
(1) AB間の距離は何kmですか。
(2) 次郎君がA地点を出発してから、B地点に着くまでにかかった時間は何時間ですか。
- 答え(1)
- 22km
- 答え(2)
- \(1\dfrac{11}{18}\)時間
- 解き方(1)
- AB間の距離を⑩とすると、太郎君がB地点に着いたとき、次郎君はA地点から①の地点まで進んでおり、残りの距離は⑨となる。B地点で太郎君を降ろし、引き返して次郎君を乗せてB地点に戻るまでにタクシーがかかった時間は1時間なので、移動した距離は36kmである、すなわち次郎君を乗せたのはB地点から18kmの地点となる。よって、次郎君が、タクシーがB地点から引き返して次郎君を乗せるまでに進んだ距離は1.8kmとなる。
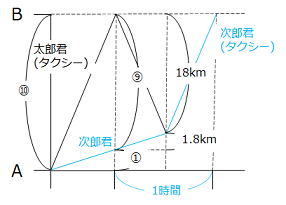
⑨ = 18 + 1.8 = 19.8
① = 2.2(km)
よって、AB間の距離は22km
- 解き方(2)
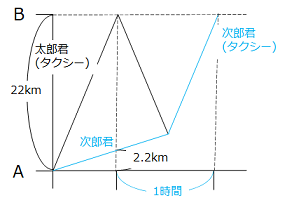
\(\dfrac{2.2}{3.6}\) + 1 = \(1\dfrac{11}{18}\)(時間)
