算数【基本】時計算

問１

時計算 = 速度の問題: ●長針と短針の距離は、長針と短針がつくる角度
●長針と短針の速さは、単位時間あたりに動く針の角度（角速度）で表す
長針：1時間に360度動く ⇒ 毎分6度
短針：1時間に30度動く ⇒ 毎分0.5度

（１）時計は7時20分を示しています。このとき、角㋐は何度ですか。

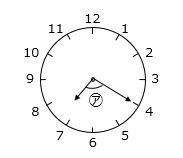
答え（１）: 100度

解き方（１）: ㋐ = 短針が作る角度 – 長針が作る角度
短針が作る角度 = 30 × 7 + 0.5 × 20 = 220(度)
長針が作る角度 = 6 × 20 = 120(度)
㋐ = 220 – 120 = 100(度)

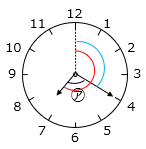
（２）ある時計が10時10分を指しています。長針と短針のつくる角のうち、小さいほうの角の大きさは何度ですか。

答え（２）: 115度

解き方（２）: 求める角度は㋐ + ㋑
㋐ = 長針がつくる角度 = 6 × 10 = 60(度)
㋑ = 360 – 短針がつくる角度
= 360 – ( 30 × 10 + 0.5 × 10 )
= 360 – 305 = 55(度)
求める角は、60 + 55 = 115(度)

問２

長針と短針が重なる問題: 旅人算と考えればわかりやすい。
●長針君の速度は毎分6度
●短針君の速度は毎分0.5度
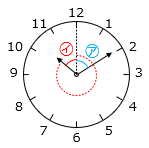
例えば1時から2時の間で重なるのであれば、ちょうど1時の時、短針君と長針君は30度離れているから
30 ÷ ( 6 – 0.5 ) = \(5\dfrac{5}{11}\)
なので、1時 \(5\dfrac{5}{11}\)分に重なる。

（１）時計の長針と短針がちょうど重なるのは、3時何分ですか。

答え（１）: \(16\dfrac{4}{11}\) 分

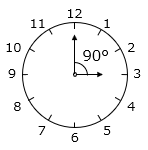
解き方（１）: 3時ちょうどのとき、長針と短針の距離は90度である。
長針の速さは毎分6度、短針の速さは毎分0.5度より、長針が短針に重なるまでにかかる時間は、
90 ÷ ( 6 – 0.5 )
= 90 ÷ 5.5
= 90 ÷ \(\dfrac{55}{10}\)
= 90 × \(\dfrac{10}{55}\)
= \(\dfrac{180}{11}\) = \(16\dfrac{4}{11}\)(分)
よって、3時 \(16\dfrac{4}{11}\) 分

（２）時刻は2時20分です。次に、今の短針と長針のつくる角が2倍の大きさになるのは何時何分何秒ですか。ただし、つくる角は小さいほうの角を考えるものとします。

答え（２）: 2時29分 \(5\dfrac{5}{11}\) 秒

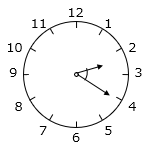
解き方（２）: 今の時刻の小さいほうの角度は、長針がつくる角度 – 短針がつくる角度。よって、
6 × 20 – ( 30 × 2 + 0.5 × 20 )
= 120 – 70 = 50(度)
長針が短針からさらに50度進むのにかかる時間は、
50 ÷ ( 6 – 0.5 )
= 50 ÷ 5.5
= 50 ÷ \(\dfrac{55}{10}\)
= 50 × \(\dfrac{10}{55}\)
= \(\dfrac{100}{11}\) = \(9\dfrac{1}{11}\)(分) = 9分 \(5\dfrac{5}{11}\) 秒
よって、2時29分 \(5\dfrac{5}{11}\) 秒

（３）8時から9時の間で、最初に短針と長針の間の角度が42°になりました。次に42°になるまで何分かかりますか。

答え（３）: \(15\dfrac{3}{11}\) 分

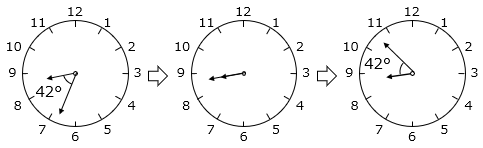
解き方（３）: 8時から9時の間で、最初に短針と長針の間の角度が42°になるとき、長針は短針より後ろにある。次に42°になるとき、長針は短針より前にある。
（長針と短針の位置関係が重要であり、正確な時間を求める必要はない）
すなわち、長針は短針まで42°追いつき、さらに追いこして42°引き離すと考えられる。
長針の速さは毎分6°、短針の速さは毎分0.5°
よって、かかる時間は、
42 ÷ ( 6 – 0.5 ) + 42 ÷ ( 6 – 0.5 )
= 84 ÷ ( 6 – 0.5 )
= 84 ÷ 5.5
= 84 ÷ \(\dfrac{55}{10}\)
= 84 × \(\dfrac{10}{55}\)
= \(\dfrac{168}{11}\) = \(15\dfrac{3}{11}\)(分)

（４）図のように文字盤が正八角形の時計があります。この正八角形の各頂点をA、B、C、D、E、F、G、Hとします。短針がAを指してからCを指すまでに、何時間何分かかりますか。

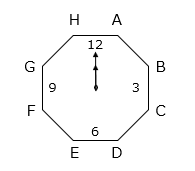
答え（４）: 3時間

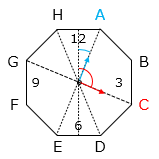
解き方（４）: 針が八角形の1辺を進む角度は 360 ÷ 8 = 45(°)
長針の速さは毎分6°、短針の速さは毎分0.5°
短針が12時からAに来るまでに進んだ角度は 22.5°である。かかった時間は、
22.5 ÷ 0.5 = 45(分)
よって、このときの時刻は 12時45分。
短針が12時からCに来るまでに進んだ角度は 22.5 + 45 × 2 = 112.5(°)である。かかった時間は、
112.5 ÷ 0.5 = 225(分) = 3時間45分
よって、このときの時刻は 3時45分。
短針がAを指してからCを指すまでにかかった時間は、3時間