算数【応用】割合

問１

赤、青、白の3色の玉が全部で612個あります。赤玉の個数は全体の \(\dfrac{1}{3}\)、青玉の個数は全体の \(\dfrac{2}{9}\) です。このとき、白玉は何個ありますか。

答え

272個

解き方

全体の個数を3と9の最小公倍数である⑨とすると、赤玉は ⑨ × \(\dfrac{1}{3}\) = ③、青玉は ⑨ × \(\dfrac{2}{9}\) = ②、白玉は ⑨ – (③ + ②) = ④となる。よって、白玉の個数は、
④ = 4 × \(\dfrac{612}{9}\) = 272(個)

問２

5000円の品物を買うのに、代金の \(\dfrac{3}{5}\) を兄が、兄が出した金額の \(\dfrac{1}{2}\) を妹が出し、残りを母が出しました。妹が出した金額はいくらですか。

答え

1500円

解き方

品物の代金を5と2の最小公倍数である⑩とすると、妹が出した金額は ⑩ × \(\dfrac{3}{5}\) × \(\dfrac{1}{2}\) = ③となる。よって、
③ = 3 × \(\dfrac{5000}{10}\) = 1500(円)

問３

AグループとBグループがあります。Bグループの人数はAグループの人数の \(\dfrac{5}{6}\) です。Aグループでは、人数の半分がねこを飼っています。Bグループでは、人数の \(\dfrac{1}{3}\) がねこを飼っています。AグループとBグループのねこを飼っている人数の比を求めなさい。

答え

9 : 5

解き方

Aグループの人数を1とすると、AグループとBグループのねこを飼っている人数の比は、
A : B = 1 × \(\dfrac{1}{2}\) : 1 × \(\dfrac{5}{6}\) × \(\dfrac{1}{3}\) = 9 : 5

問４

ある商品を買い、代金を8回に分けて支払うことにしました。初回のみ代金の \(\dfrac{1}{6}\) を払い、残りは同じ額で支払いました。代金に対する5回目までに支払った合計額の割合を求めなさい。

答え

\(\dfrac{9}{14}\)

解き方

2回目以降の1回の支払金額の割合は、(1 – \(\dfrac{1}{6}\) ) × \(\dfrac{1}{7}\) = \(\dfrac{5}{42}\)
5回目までに支払った合計額の割合は、
\(\dfrac{1}{6}\) + \(\dfrac{5}{42}\) × 4 = \(\dfrac{9}{14}\)

問５

Aさんはいくつかのビー玉を持っています。はじめに持っていたビー玉の \(\dfrac{3}{7}\) を妹にあげ、弟に残りの \(\dfrac{3}{7}\) をあげました。さらに6個を弟にあげたところ、残りは10個になりました。Aさんがはじめに持っていたビー玉は何個ですか。

答え

49個

解き方

Aさんがはじめに持っていたビー玉の個数を、問題文の分母7 × 7の \(\boxed{49}\) とすると、妹にあげた個数は \(\boxed{49}\) × \(\dfrac{3}{7}\) = \(\boxed{21}\)、弟にあげた個数は ( \(\boxed{49}\) – \(\boxed{21}\) ) × \(\dfrac{3}{7}\) + 6 = \(\boxed{12}\) + 6 となる。

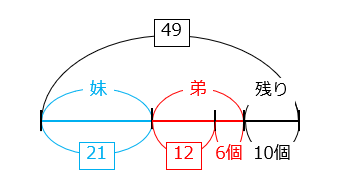
\(\boxed{49}\) – ( \(\boxed{21}\) + \(\boxed{12}\) ) = 6 + 10
\(\boxed{1}\) = 1
\(\boxed{49}\) = 1 × 49 = 49(個)

問６

ある本を、1日目は全体の \(\dfrac{4}{9}\)、2日目は残りの \(\dfrac{3}{7}\)、3日目は120ページ読んで全部読み終わりました。全部で何ページありましたか。

答え

378ページ

解き方

全ページ数を9と7の最小公倍数である \(\boxed{63}\) とすると、1日目に読んだのは \(\boxed{63}\) × \(\dfrac{4}{9}\) = \(\boxed{28}\)、2日目に読んだのは ( \(\boxed{63}\) – \(\boxed{28}\) ) × \(\dfrac{3}{7}\) = \(\boxed{15}\)

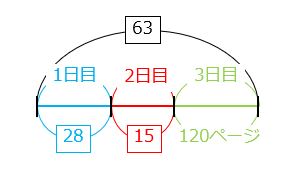
\(\boxed{63}\) – ( \(\boxed{28}\) + \(\boxed{15}\) ) = 120
\(\boxed{1}\) = 6
よって全ページ数は、\(\boxed{63}\) = 6 × 63 = 378(ページ)

問７

ある中学校で入学試験を行ったところ、合格者数は受験者数の \(\dfrac{11}{21}\) より3人少なく、不合格者数は受験者数の \(\dfrac{7}{15}\) より7人多かったです。このとき、受験者数は何人でしたか。

答え

420人

解き方

受験者数を21と15の最小公倍数である \(\boxed{105}\) とすると、合格者は \(\boxed{105}\) × \(\dfrac{11}{21}\) – 3 = \(\boxed{55}\) – 3、不合格者は \(\boxed{105}\) × \(\dfrac{7}{15}\) + 7 = \(\boxed{49}\) + 7
合格者と不合格者の和が受験者数なので、
\(\boxed{55}\) – 3 + \(\boxed{49}\) + 7 = \(\boxed{105}\)
\(\boxed{1}\) = 4
よって受験者数は、\(\boxed{105}\) = 4 × 105 = 420(人)

問８

A君はペットボトルの水を全体の \(\dfrac{2}{5}\) 飲み、B君は300mLを飲みました。C君が残りの \(\dfrac{5}{9}\) を飲んだところ120mL残りました。最初にペットボトルに入っていた水は何mLですか。

答え

950mL

解き方

ペットボトルの水の分け方を線分図で示した。

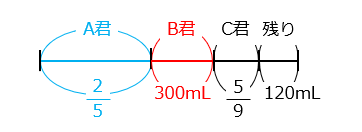
残りの120mLが \(\dfrac{4}{9}\) にあたるので、C君が飲んだ量と残りの合計は、120 × \(\dfrac{9}{4}\) = 270(mL)
270mLと300mLが全体の \(\dfrac{3}{5}\) にあたる。
よって最初にペットボトルに入っていた水は、(270 + 300) × \(\dfrac{5}{3}\) = 950(mL)

問９

ある本を、1日目は30ページ読み、2日目は残りの \(\dfrac{2}{5}\) を読んだところ、2日間で全体の \(\dfrac{8}{17}\) を読んだことになりました。この本は全部で何ページありますか。

答え

255ページ

解き方

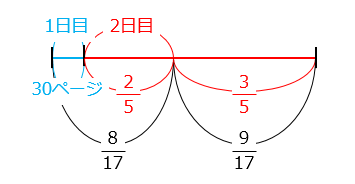
全ページ数を⑰とすると、2日間で読んだページ数は ⑰ × \(\dfrac{8}{17}\) = ⑧、残りのページ数は⑨となり、これが2日目に読んだあとの残りのページ数に当たる。よって、1日目に読んだ後の残りのページ数は ⑨ × \(\dfrac{5}{3}\) = ⑮となる。

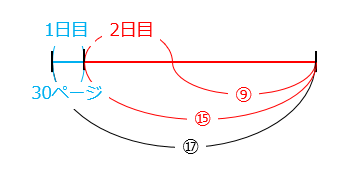
⑰ – ⑮ = ② ‣‣‣ 30ページ
① = 15
全ページ数は、⑰ = 17 × 15 = 255

問１０

浴槽に全体の \(\dfrac{3}{5}\) だけ水が入っています。その水の \(\dfrac{1}{3}\) をすて、120Lの水を入れると、入っている水は浴槽全体の \(\dfrac{2}{3}\) になりました。浴槽が満水のときは何L入りますか。

答え

450L

解き方

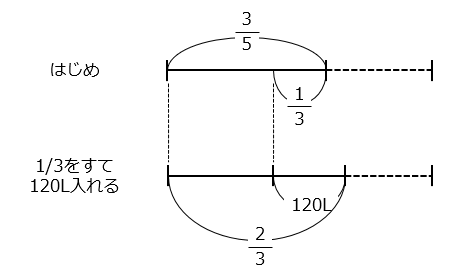
浴槽が満水のときの水の量を3と5の最小公倍数である⑮とすると、はじめに入っていた水の量は ⑮ × \(\dfrac{3}{5}\) = ⑨、すてた水の量は ⑨ × \(\dfrac{1}{3}\) = ③となり、残っている量は⑥となる。ここに120L入れた量は、⑮ × \(\dfrac{2}{3}\) = ⑩となる。

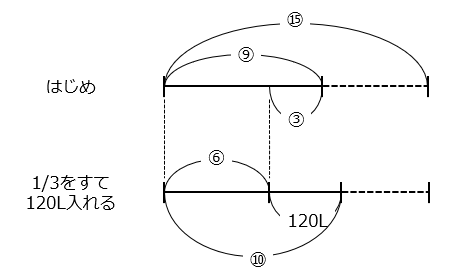
⑩ – ⑥ = ④ ‣‣‣ 120L
① = 30
満水のときの水の量は、⑮ = 15 × 30 = 450(L)

問１１

Aさんはあめをいくつか持っています。持っていたあめの \(\dfrac{1}{3}\) をBさんにあげ、次に残ったあめの\(\dfrac{1}{2}\) をCさんにあげ、最後に残ったあめの \(\dfrac{2}{3}\) をDさんにあげたところ、あめは2個残りました。最初にAさんが持っていたあめは何個ですか。

答え

18個

解き方

Aさんが最初に持っていたあめの個数を3と2の最小公倍数である⑥とすると、Bさんにあげた個数は ⑥ × \(\dfrac{1}{3}\) = ②、Cさんにあげた個数は (⑥ – ②) × \(\dfrac{1}{2}\) = ②、Dさんにあげた個数は (⑥ – ② – ②) × \(\dfrac{2}{3}\) = \(\dfrac{④}{3}\) となる。よって、
⑥ – ② – ② – \(\dfrac{④}{3}\) = 2
⑱ – ⑥ – ⑥ – ④ = 6
① = 3
最初にAさんが持っていたあめは、⑥ = 6 × 3 = 18(個)

問１２

ある本を、1日目は28ページ読み、2日目は全体の \(\dfrac{1}{18}\)、3日目は全体の \(\dfrac{1}{9}\) を読んだら、残ったページは全体の \(\dfrac{7}{9}\) より8ページ少なくなりました。この本は全部で何ページありますか。

答え

360ページ

解き方

全ページ数を18と9の最小公倍数である⑱とすると、2日目に読んだページ数は ⑱ × \(\dfrac{1}{18}\) = ①、3日目に読んだページ数は ⑱ × \(\dfrac{1}{9}\) = ②、残ったページ数は ⑱ × \(\dfrac{7}{9}\) – 8 = ⑭ – 8 となる。よって、
⑱ = 28 + ① + ② + ⑭ – 8
① = 20
この本の全ページ数は、⑱ × 20 = 360(ページ)

問１３

A君は持っているお金の半分より70円少ないお金を使い、次に残りのお金の半分より70円多く使ったら、490円残りました。A君がはじめに持っていたお金はいくらですか。

答え

2100円

解き方

半分とは \(\dfrac{1}{2}\) のことである。A君がはじめに持っていたお金を②とすると、はじめに使ったお金は ② × \(\dfrac{1}{2}\) – 70 = ① – 70、次に使ったお金は {② – (① – 70)} × \(\dfrac{1}{2}\) + 70 となる。

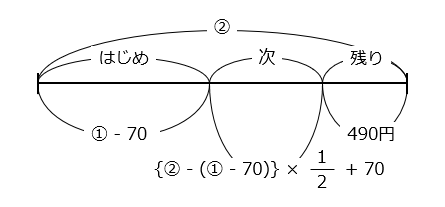
② – 490 = ① – 70 + {② – (① – 70)} × \(\dfrac{1}{2}\) + 70
② – 490 = ① + ① – (① – 70) × \(\dfrac{1}{2}\)
(① – 70) × \(\dfrac{1}{2}\) = ① + ① – ② + 490
① – 70 = 980
① = 1050
A君がはじめに持っていたお金は、② = 2 × 1050 = 2100(円)

問１４

ある中学校では男子と女子の人数の比は 3：2 で、自転車で通学している人は全体の18%です。自転車で通学している男子は180人、自転車で通学している女子は全体の \(\dfrac{3}{50}\) です。このとき、自転車で通学していない女子は何人いますか。

答え

510人

解き方

男子の人数を \(\boxed{3}\) とすると、女子の人数は \(\boxed{2}\)、全体の人数は \(\boxed{5}\) と表すことができる。
自転車で通学している女子の人数は2つの式で表すことができる。
①自転車で通学している人は全体の18%で、自転車で通学している男子は180人 ⇒ \(\boxed{5}\) × 0.18 – 180
②自転車で通学している女子は全体の \(\dfrac{3}{50}\) ⇒ \(\boxed{5}\) × \(\dfrac{3}{50}\)

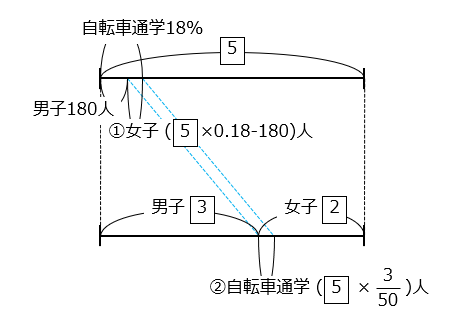
①と②は等しいので、
\(\boxed{5}\) × 0.18 – 180 = \(\boxed{5}\) × \(\dfrac{3}{50}\)
\(\boxed{0.9}\) – 180 = \(\boxed{0.3}\)
\(\boxed{0.6}\) = 180
\(\boxed{1}\) = 300
より、全体の人数は \(\boxed{5}\) = 5 × 300 = 1500(人)、女子の人数は \(\boxed{2}\) = 2 × 300 = 600(人) となる。自転車で通学していない女子は、
600 – 1500 × \(\dfrac{3}{50}\) = 600 – 90 = 510(人)