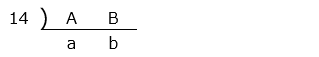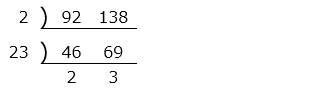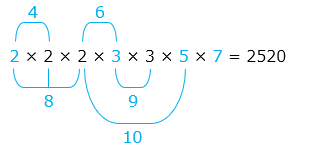算数【入試】約数・倍数・素数

問１

126 の約数について、次の問いに答えなさい。

（１）約数の個数を求めなさい。

答え（１）: 12 個

解き方（１）: 126 の約数を書き出すと、
1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126
よって、12 個

【別解】素因数分解して求める
126 = 2 × 3 × 3 × 7 より、2 が 1 個、3 が 2 個、7 が 1 個
よって約数の個数は、
( 1 + 1 ) × ( 2 + 1 ) × ( 1 + 1 )
= 2 × 3 × 2 = 12 [個]
今回は（２）ですべての約数の和を求めるのですべての約数を書き出す必要があるが、この方法を知っていれば、書き出し忘れがないことを確認できる。

（２）すべての約数の和を求めなさい。

答え（２）: 312

解き方（２）: 1 + 2 + 3 + 6 + 7 + 9 + 14 + 18 + 21 + 42 + 63 + 126
= ( 126 + 14 ) + ( 63 + 7 ) + ( 42 + 2 + 6 ) + ( 21 + 9 ) + 18 + 3 + 1
= 140 + 70 + 50 + 30 + 22 = 312

問２

2 つの分数 \(\dfrac{3}{4}\) と \(\dfrac{5}{7}\) について、答えなさい。

（１）2 つの分数のうち、大きいほうの分数を答えなさい。

答え（１）: \(\dfrac{3}{4}\)

解き方（１）: 分母を最小公倍数でそろえて、分子の大きさを比較する。
\(\dfrac{3}{4}\) = \(\dfrac{21}{28}\)
\(\dfrac{5}{7}\) = \(\dfrac{20}{28}\)
21 ＞ 20 より、大きいのは \(\dfrac{3}{4}\)

（２）2 つの分数のあいだの数で、分数で表すと分母が 84 であり、分母と分子の最大公約数が 1 であるものを答えなさい。

答え（２）: \(\dfrac{61}{84}\)

解き方（２）: 2 つの分数の分母を 84 とすると、\(\dfrac{3}{4}\) = \(\dfrac{63}{84}\)、\(\dfrac{5}{7}\) = \(\dfrac{60}{84}\) となる。
求める分数は分母と分子の最大公約数が 1 より、分子は素数と考えられる。
63 と 60 のあいだの数で素数は 61 のみなので、\(\dfrac{61}{84}\)

（３）横の長さが \(\dfrac{3}{4}\) m、縦の長さが \(\dfrac{5}{7}\) m のタイルを向きをかえずに敷きつめて正方形を作るとき、最低何枚必要か答えなさい。

答え（３）: 420 枚

解き方（３）: 最も小さい正方形の 1 辺の長さは \(\dfrac{3}{4}\) と \(\dfrac{5}{7}\) の最小公倍数となる。
（１）より、分母を 28 でそろえると分子は 21 と 20 となり、分子の最小公倍数は 21 × 20 = 420 となる。よって、\(\dfrac{3}{4}\) と \(\dfrac{5}{7}\) の最小公倍数は \(\dfrac{420}{28}\) = 15
正方形の 1 辺の長さは 15 m なので、必要なタイルの枚数は、
( 15 ÷ \(\dfrac{3}{4}\) ) × ( 15 ÷ \(\dfrac{5}{7}\) )
= ( 15 × \(\dfrac{4}{3}\) ) × ( 15 × \(\dfrac{7}{5}\) )
= 20 × 21 = 420 [枚]

問３

\(8\dfrac{2}{5}\) にかけても \(3\dfrac{1}{9}\) にかけても整数となる最も小さい分数を求めなさい。

答え: \(3\dfrac{3}{14}\)

解き方: \(8\dfrac{2}{5}\) = \(\dfrac{42}{5}\)、\(3\dfrac{1}{9}\) = \(\dfrac{28}{9}\) より、求める分数は、
\(\dfrac{5\ と\ 9\ の最小公倍数}{42\ と\ 28\ の最大公約数}\) = \(\dfrac{45}{14}\) = \(3\dfrac{3}{14}\)

問４

100 から 500 までの整数のうち 7 の倍数の個数を求めなさい。

答え: 57個

解き方: 1 から 99 までの整数のうち 7 の倍数は 99 ÷ 7 = 14. … ⇒ 14 個
1 から 500 までの整数のうち 7 の倍数は 500 ÷ 7 = 71. … ⇒ 71 個
よって求める個数は 71 – 14 = 57 個

問５

4 つの約数を持つ整数のうち、最も小さい整数を答えなさい。

ヒント: ある整数の約数の個数は、素因数分解したときのそれぞれの素数の個数に 1 を加えたものをかけ合わせることで求めることができる
例えば 18 は 2 × 3 × 3 であり、2 は 1 つなので ( 1 + 1 )、3 は 2 つなので ( 2 + 1 )となり、( 1 + 1 ) × ( 2 + 1 ) = 6 となる
したがって、4 つの約数を持つ整数は〇 × △（ ( 1 + 1 ) × ( 1 + 1 ) = 4 ）、または □ × □ × □（ 3 + 1 = 4 ）で表すことができる（〇、△、□ はすべて素数）

答え: 6

解き方: 4 つの約数を持つ整数は〇 × △、または □ × □ × □ で表すことができる（〇、△、□ はすべて素数）
〇 × △ で最も小さいのは 2 × 3 = 6
□ × □ × □ で最も小さいのは 2 × 2 × 2 = 8
6 ＜ 8 より、6

問６

1 から 1000 までの整数のうち、約数が 5 個ある整数は全部で \(\boxed{ア}\) 個あり、その和は \(\boxed{イ}\) です。空欄に当てはまる数を答えなさい。

ヒント: ある整数の約数の個数は、素因数分解したときのそれぞれの素数の個数に 1 を加えたものをかけ合わせることで求めることができる
例えば 18 は 2 × 3 × 3 であり、2 は 1 つなので ( 1 + 1 )、3 は 2 つなので ( 2 + 1 )となり、( 1 + 1 ) × ( 2 + 1 ) = 6 となる
したがって、5 つの約数を持つ整数は〇 × 〇 × 〇 × 〇（ 4 + 1 = 5 ）で表すことができる（〇は同じ素数）

答え: ア：3　イ：722

解き方: ア：5 つの約数を持つ整数は〇 × 〇 × 〇 × 〇で表すことができる（〇は同じ素数）
〇 = 2 のとき 16
〇 = 3 のとき 81
〇 = 5 のとき 625
〇 = 7 のとき 2401 ＞ 1000
よって、ア = 3

イ：16 + 81 + 625 = 722

問７

2 けたの整数が 2 つあります。この 2 つの整数の最大公約数が 14、最小公倍数が 168 であるとき、この2つの整数を答えなさい。

答え: 42 と 56

解き方: 求める 2つの整数をそれぞれ A、B とし、A、B をそれぞれ最大公約数 14 で割った商を a、b ( a、b は互いに素 ) とする。これをすだれ算であらわすと、以下のようになる。

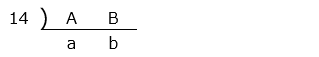
最小公倍数は、14 × a × b = 168 より a × b = 168 ÷ 14 = 12 となる。これを満たす互いに素となる ( a, b ) の組は ( 1, 12 ) と ( 3, 4 ) がある。
( a, b ) = ( 1, 12 ) のとき、A = 14 × 1 = 14、 B = 14 × 12 = 168 ⇒ A、B は 2 けたの整数：×
( a, b ) = ( 3, 4 ) のとき、A = 14 × 3 = 42、 B = 14 × 4 = 56

問８

縦の長さが 92 cm、横の長さが 138 cmの長方形のタイルがあります。このタイルを余りを出さないように、最も大きい正方形に切り分けたとき、正方形の一辺の長さは何 cmか答えなさい。

答え: 46 cm

解き方: 正方形の 1 辺の長さは 92 と 138 の最大公約数となる。

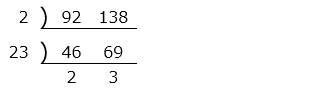
よって、2 × 23 = 46 [cm]

問９

1234 に「ある整数」を足すと 2 ～ 10 のどの整数でも割り切れます。「ある整数」のうち、最も小さい整数を答えなさい。

答え: 1286

解き方: 2 ～ 10 のどの整数でも割り切れる整数は

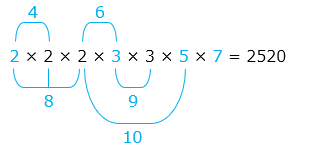
の倍数
よって、ある整数は 2520 – 1234 = 1286

問１０

2 けたの整数が 2 つあります。この 2 つの整数の積は 7020、最大公約数は 6 です。この 2 つの整数を求めなさい。

答え: 78 と 90

解き方: 求める 2つの整数をそれぞれ A、B とし、A、B をそれぞれ最大公約数 6 で割った商を a、b ( a、b は互いに素 ) とする。これをすだれ算であらわすと、以下のようになる。

A = 6 × a、B = 6 × b となり、

となる。よって、最小公倍数は 7020 ÷ 6 = 1170
したがって、6 × a × b = 1170 より a × b = 1170 ÷ 6 = 195 となる。これを満たす互いに素となる ( a, b ) の組は ( 1, 195 ) 、 ( 5, 39 )、 ( 13, 15 ) がある。
( a, b ) = ( 1, 195 ) のとき、A = 6 × 1 = 6、 B = 6 × 195 ≠ 2 けたの整数 ⇒ ×
( a, b ) = ( 5, 39 ) のとき、A = 6 × 5 = 30、 B = 6 × 39 ≠ 2 けたの整数 ⇒ ×
( a, b ) = ( 13, 15 ) のとき、A = 6 × 13 = 78、 B = 6 × 15 = 90